树

发表于 更新于 分类于 阅读次数：

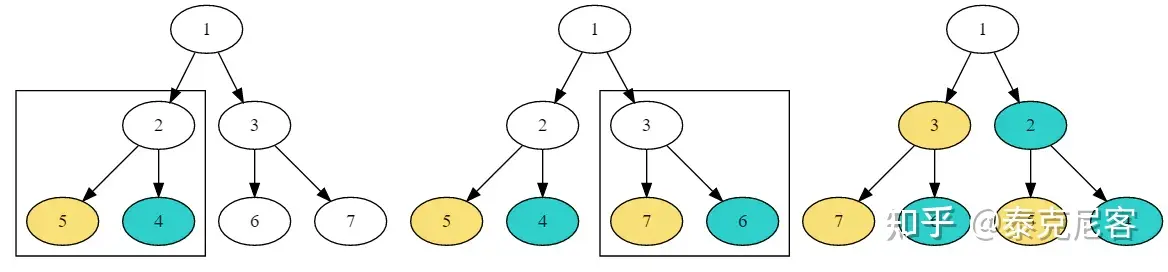
二叉树问题思考角度就是站到ROOT节点，思考我要让左右节点返回给我什么信息。然后思考我有了这个信息后要干什么

路径总和 III[12]

数组情况：和为k的子数组

思路：

  1. 暴力，以每个节点为起点出发，然后直接遍历到终点。两层for循环
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    //暴力
    int res = 0;
    long targetSum = 0;
    public int pathSum(TreeNode root, int _targetSum) {
        //暴力搜索，类似于我们 普通前缀和的 两层for循环
        targetSum = (long)_targetSum;
        t1(root);
        return res;
    }
    public void t1(TreeNode root){
        if(root == null) return;
        //起点
        traverse(root, 0);
        t1(root.left);
        t1(root.right);
    }
    public void traverse(TreeNode root,long curSum){
        if(root == null){
            return;
        }
        curSum+=root.val;
        if(curSum == targetSum) res++;
        traverse(root.left, curSum);
        traverse(root.right, curSum);
    }

}
  1. 前缀和+ 两数之和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    //暴力
    int res = 0;
    long targetSum = 0;
    //只针对单一个数
    //k：前缀和 v：相同前缀和的个数
    Map<Long, Integer> preSumCounter = new HashMap<>();

    public int pathSum(TreeNode root, int _targetSum) {
        //前缀和 + 两数之和
        targetSum = (long) _targetSum;
        preSumCounter.put(0L, 1); // 前缀和为0的次数为1
        traverse(root, 0);
        return res;
    }

    public void traverse(TreeNode root, long curSum) {
        if (root == null) {
            return;
        }
        curSum += root.val;
        // preSum - xx = targetSum
        // preSum - targetSum = xx
        //即在map里找是否有 树为 presum + (-targetSum)
        res += preSumCounter.getOrDefault(curSum + (-targetSum), 0);
        //更新前缀和
        preSumCounter.put(curSum, preSumCounter.getOrDefault(curSum, 0) + 1);

        traverse(root.left, curSum);
        traverse(root.right, curSum);
        
        //回退
        preSumCounter.put(curSum, preSumCounter.get(curSum) - 1);
    }

}

二叉树中的最大路径和[173]

思路

  1. 站在ROOT节点思考左右节点要返回给我什么信息？我希望左子节点返回给我左子树的最大路径和。右节点类似
  2. 思考有了这个信息要干什么。无非就是求出最大路径和
    四种情况
    leftSum + cur.val

rightSum + cur.val

cur.val

cur.val + leftSum + rightSum

画板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int res = Integer.MIN_VALUE;
    public int maxPathSum(TreeNode root) {
        dfs(root);
        return res;
    }
    public int dfs(TreeNode cur){
        if(cur == null) return 0;
        int leftSum = dfs(cur.left);
        int rightSum = dfs(cur.right);
        //子树的返回
        int ret = Math.max(cur.val, Math.max(leftSum,rightSum) + cur.val);
        //最终结果
        res = Math.max(res, Math.max(ret, cur.val + leftSum + rightSum));
        return ret;
    }
}

二叉树的最近公共祖先[251]

思路：

法一：DFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        //法一 dfs
        return dfs(root, p, q);
    }

    public TreeNode dfs(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null) {
            return root;
        }
        if (root == p || root == q)
            return root;
        TreeNode left = dfs(root.left, p, q);
        TreeNode right = dfs(root.right, p, q);
        if (left == null)
            return right;
        if (right == null)
            return left;
        if (left == right)
            return root;
        //p,q都没找到
        return root;
    }
}

法二：Map存子节点->父节点，然后转换成相交链表问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    //k：子节点 v：父节点
    Map<TreeNode, TreeNode> map = new HashMap<>();

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        dfs(root, null);
        //q节点的祖先 集合
        Set<TreeNode> qZX = new HashSet<>();
        while (q != null) {
            qZX.add(q);
            q = map.get(q);
        }

        while (p != null) {
            //相交节点
            if (qZX.contains(p)) {
                return p;
            }
            p = map.get(p);
        }
        return null;
    }

    //
    public void dfs(TreeNode cur, TreeNode par) {
        if (cur == null) {
            return;
        }
        map.put(cur, par);
        dfs(cur.left, cur);
        dfs(cur.right, cur);
    }
}

时间复杂度都是O( N )

对称二叉树[91]

思路：

1. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
	public boolean isSymmetric(TreeNode root) {
		if(root==null) {
			return true;
		}
		//调用递归函数，比较左节点，右节点
		return dfs(root.left,root.right);
	}
	
	boolean dfs(TreeNode left, TreeNode right) {
		//递归的终止条件是两个节点都为空
		//或者两个节点中有一个为空
		//或者两个节点的值不相等
		if(left==null && right==null) {
			return true;
		}
		if(left==null || right==null) {
			return false;
		}
		if(left.val!=right.val) {
			return false;
		}
		//再递归的比较 左节点的左孩子 和 右节点的右孩子
		//以及比较  左节点的右孩子 和 右节点的左孩子
		return dfs(left.left,right.right) && dfs(left.right,right.left);
	}
}

作者：王尼玛
链接：https://leetcode.cn/problems/symmetric-tree/solutions/46560/dong-hua-yan-shi-101-dui-cheng-er-cha-shu-by-user7/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

翻转二叉树[67]

思路：

  1. 翻转左右子节点就好，然后就交给递归函数了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
        return dfs(root);
    }

    public TreeNode dfs(TreeNode root) {
        if (root == null)
            return null;
        TreeNode left = dfs(root.left);
        TreeNode right = dfs(root.right);
        //在根节点 交换左右子节点即可
        root.left = right;
        root.right = left;

        return root;
    }
}

二叉树的最大深度[87]

思路（DFS）：

  1. if(root.left == null && root.right == null) 结果更新时

思路（BFS）:

  1. 层序遍历，每过一层 depth++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    //int cnt = 0;
    int res = Integer.MIN_VALUE;
    public int maxDepth(TreeNode root) {
        if(root != null){
            dfs(root,1);
            return res;
        }
        return 0;
    }
    public void dfs(TreeNode root,int cnt){
        if(root == null) {
            return ;
        }
        if(root.left == null && root.right == null){
            res = Math.max(res,cnt);
            return;
        }
        dfs(root.left,cnt + 1);
        dfs(root.right,cnt + 1);
    }
}

BFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        ArrayDeque<TreeNode> q = new ArrayDeque();
        if (root != null)
            q.add(root);
        int depth = 0;
        while (!q.isEmpty()) {
            int size = q.size();
            while (size > 0) {
                TreeNode cur = q.remove();
                if (cur.left != null) {
                    q.add(cur.left);
                }
                if (cur.right != null) {
                    q.add(cur.right);
                }
                size--;
            }
            depth++;
        }
        return depth;
    }
}

二叉树的直径[79]

思路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int res = 0;

    public int diameterOfBinaryTree(TreeNode root) {
        dfs(root);
        return res;
    }
    //也是站在当前根节点 思考 左右子节点要给我返回什么
    public int dfs(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int lM = dfs(root.left);
        int rM = dfs(root.right);
        res = Math.max(lM + rM, res);
        // 这个 1 是指Cur节点返回给上一级的时候，要把cur节点 加上去
        return Math.max(lM, rM) + 1;
    }
}

验证二叉搜索树[79]

思路：

  1. 二叉搜索树 中序遍历 为 单调递增数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    List<Integer> list = new ArrayList();

    public boolean isValidBST(TreeNode root) {
        f1(root);
        for (int i = 1; i < list.size(); i++) {
            if (list.get(i) <= list.get(i - 1)) {
                return false;
            }
        }
        return true;
    }
    //二叉搜索树 中序遍历 为 单调递增数组
    public void f1(TreeNode root) {
        if (root == null) {
            return;
        }
        f1(root.left);
        list.add(root.val);
        f1(root.right);
    }
}

二叉树的序列化与反序列化[57]

思路：

  1. 序列化容易，就是前序遍历，转成字符串，或者层序遍历
  2. 反序列化比较难，一种是bfs，一种是dfs
  3. 就是你序列化以BFS，你反序列化就是要BFS。DFS同样
  4. 题目其实就是给你root，序列化成字符串，然后再根据字符串反序列为树

DFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Codec {
    StringBuilder serRes = new StringBuilder();
    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
        f1(root);
        return serRes.toString();
    }
    public void f1(TreeNode root){
        if(root == null){
            serRes.append("null,");
            return;
        }
        else serRes.append(root.val + ",");
        f1(root.left);
        f1(root.right);
    }

    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {
        String []datas = data.split(",");
        return builder(datas);
    }
    //构建树
    int index = 0;

    public TreeNode builder(String[] data){
        //看示例1 即 从上到下，从右倒左遍历
        String curV = data[index];
        index++;
        //当前节点
        TreeNode curNode = null;
        if(curV.equals("null")){
            return curNode;
        } 
        else {
            int curVN = Integer.parseInt(curV);
            curNode = new TreeNode(curVN);
            //左右子节点 交给子树去构造，相信递归
            curNode.left = builder(data);
            curNode.right = builder(data);
        }

        return curNode;

    }
}

// Your Codec object will be instantiated and called as such:
// Codec ser = new Codec();
// Codec deser = new Codec();
// TreeNode ans = deser.deserialize(ser.serialize(root));

BFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Codec {
    StringBuilder serRes = new StringBuilder();

    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
        Queue<TreeNode> q = new LinkedList<>();
        q.add(root);
        while (!q.isEmpty()) {
            TreeNode cur = q.poll();
            if (cur != null) {
                serRes.append(cur.val).append(",");
                q.add(cur.left);
                q.add(cur.right);
            } else {
                serRes.append("null,");
            }
        }
        return serRes.toString();

    }

    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {

        String[] datas = data.split(",");

        return builder(datas);
    }

    //构建树
    public TreeNode builder(String[] data) {

        if (data.length == 0 || data[0].equals("null")) {
            return null;
        }
        TreeNode res = new TreeNode(Integer.parseInt(data[0]));
        Queue<TreeNode> q = new LinkedList<>();
        q.add(res);
        int index = 1;
        while (!q.isEmpty()) {
            TreeNode curNode = q.poll();
            if (!data[index].equals("null")) {
                curNode.left = new TreeNode(Integer.parseInt(data[index]));
                q.add(curNode.left);
            }
            index++;
            if (!data[index].equals("null")) {
                curNode.right = new TreeNode(Integer.parseInt(data[index]));
                q.add(curNode.right);
            }
            index++;
        }
        return res;
    }
}

// Your Codec object will be instantiated and called as such:
// Codec ser = new Codec();
// Codec deser = new Codec();
// TreeNode ans = deser.deserialize(ser.serialize(root));

二叉树展开为链表[43]

思路：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    TreeNode pre=null;
    public void flatten(TreeNode root) {
        if(root==null) return;

        if(pre!=null){
            pre.right=root;
        }
        //提前保存一下即可，防止丢失子树
        TreeNode tmp=root.right;
        pre=root;
        flatten(root.left);
        flatten(tmp);
        root.left=null;
    }
}

不同的二叉搜索树[31]

背诵题

思路：

  1. 找规律，先找出 比如 1个节点（n=1），2,….的时候，这时候有多少种二叉搜索树
  2. 然后再找 n和n-1的关系，即递归公式

明确它的一个dp数组含义了，即 第i个节点 有多少种二叉搜索树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int numTrees(int n) {
        //1: 1
        //2: 2
        //3: 5
        //dp数组含义：n = i时有多少种二叉搜索树

        ////如果整数1 ~ n中的 k 作为根节点值，则 1 ~ k-1 会去构建左子树，k+1 ~ n 会去构建右子树。!!!
        if( n <= 2) return n;
        int []dp = new int[n+1];
        dp[0] = 1;
        dp[1] = 1;
        for(int i = 2;i <= n;i++){
            //在 i 范围内，当前节点val = k 
            //如果整数1 ~ i中的 k 作为根节点值，则 1 ~ k-1 会去构建左子树，k+1 ~ i 会去构建右子树。!!!
            //此时 
            for(int k = 0;k <= i - 1;k++){
                //左 和 右 组合
                //为什么组合这里是乘法？
                dp[i] += dp[k] * dp[i - k - 1]; 
            }
        }
        return dp[n];
    }
}

1️⃣ 为什么是 乘法？

我们考虑：

如果整数 1 ~ i 中选 k 作为根节点，
左子树可以用 1 ~ k-1 构建，右子树可以用 k+1 ~ i 构建。

假设：

  • 左子树可以构建 L = dp[k] 种不同的 BST
  • 右子树可以构建 R = dp[i - k - 1] 种不同的 BST

总的 BST 数量 = 左子树方案数 × 右子树方案数

为什么是乘法？
因为每一种左子树都可以和每一种右子树组合成一个新的 BST。
这是经典的排列组合思想：左 * 右。

比如小明有4个苹果，小红有5个香蕉。他们组合是多少，那肯定是4*5

举个小例子：

  • k=2，左子树用 1 构建 → 1 种方案
  • 右子树用 3,4 构建 → 2 种方案

总的 BST 数 = 1 * 2 = 2 种。

2️⃣ dp[k] 和 dp[i - k - 1] 分别是左子树和右子树

  • dp[k] → 左子树的方案数
    因为左子树包含 k 左边的 k 个节点（1 ~ k），所以 dp[k]
  • dp[i - k - 1] → 右子树的方案数
    因为右子树包含剩下的 i - k - 1 个节点（k+1 ~ i），所以 dp[i - k - 1]

⚠️ 注意下标关系：

  • i = 当前节点总数
  • k = 左子树节点数（或根节点下标？在你的循环中，k是左子树节点数）
  • 右子树节点数 = i - k - 1

打家劫舍 III[19]

路径总和 III[]

实现 Trie (前缀树)[34]

思路：

  1. 构造26叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

class Trie {
    private static class Node {
        Node[] son = new Node[26];
        boolean end = false;
    }

    private final Node root = new Node();

    public Trie() {

    }

    public void insert(String word) {
        Node cur = root;
        for (char c : word.toCharArray()) {
            int index = c - 'a';
            //无路可走？ new 出来
            if (cur.son[index] == null) {
                cur.son[index] = new Node();
            }
            cur = cur.son[index];
        }
        cur.end = true;
    }

    public boolean search(String word) {
        return find(word) == 2;
    }

    public boolean startsWith(String prefix) {
        return find(prefix) != 0;
    }

    public int find(String word) {
        Node cur = root;
        for (char c : word.toCharArray()) {
            int index = c - 'a';
            if (cur.son[index] == null)
                return 0;
            cur = cur.son[index];
        }
        //2为找到了 1为找到前缀
        return cur.end ? 2 : 1;
    }
}

/**
 * Your Trie object will be instantiated and called as such:
 * Trie obj = new Trie();
 * obj.insert(word);
 * boolean param_2 = obj.search(word);
 * boolean param_3 = obj.startsWith(prefix);
 */

把二叉搜索树转换为累加树[4]

思路：

  1. 利用二叉搜索树的特性，中序遍历为 有序数组
  2. 然后算出中序遍历后的数组的每个的元素的后缀和
  3. 然后再次中序遍历更改 树节点的val
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    List<Integer> l = new ArrayList();
    int index = 0;
    public TreeNode convertBST(TreeNode root) {
        traverse(root);
        //System.out.println(l);
        //每个节点 node 的新值  等于  原树中大于或等于 node.val 的值之和
        int sum = 0;
        for(int i = 0;i < l.size(); i++){
            sum += l.get(i);
        }
        int preSum = 0;
        for(int i = 0; i < l.size(); i++){
            int temp = l.get(i);
            l.set(i, sum - preSum);
            preSum += temp;
        }
        generate(root);
        //System.out.println(l);
        return root;
    }
    public void traverse(TreeNode root){
        if(root == null) return;
        traverse(root.left);
        l.add(root.val);
        traverse(root.right);
    }
    public void generate(TreeNode root){
        if(root == null) return;
        generate(root.left);
        root.val = l.get(index); 
        index++;
        generate(root.right);
    }
}

合并二叉树[]

思路

  1. 前序遍历，但这样是错误，在merge时，root1 = root2，改变的不是引用！
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        dfs(root1, root2);
        return root1;
    }
    public void dfs(TreeNode root1,TreeNode root2){
        if(root1 == null && root2 == null){
            return;
        }
        else if(root1 == null && root2 != null){
            root1 = root2;
            return;
        }
        else if(root1 != null && root2 == null){
            
            return;
        }
        else if(root1 != null && root2 != null){
            root1.val += root2.val;
        }
        dfs(root1.left,root2.left);
        dfs(root1.right,root2.right);
    }
}

正确的做法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        return build(root1, root2);
    }
    //返回节点
    public TreeNode build(TreeNode root1, TreeNode root2){
        if(root1 == null && root2 == null){
            return null;
        }
        if(root1 != null && root2 == null){
            return root1;
        }
        if(root1 == null && root2 != null){
            return root2;
        }
        
        TreeNode res = new TreeNode();
        if(root1 != null && root2 != null) res.val = root1.val + root2.val; 
        res.left = build(root1.left, root2.left);
        res.right = build(root1.right, root2.right);

        return res;
    }
}