other sql db
Oracle:一个Schema是一个user,一个数据库只有一个,可以高sass玩法,数据库层面就做物理隔离了
Oracle:一个Schema是一个user,一个数据库只有一个,可以高sass玩法,数据库层面就做物理隔离了
CompleteableFuture大家都用过,里面有supply、then、combine、allOf等等方法,都可以用来接收一个任务,最终将多个任务汇总成一个结果。
但有一个问题,你supply一个任务后,这个任务就黑盒了。如果你编排了很多个任务,每一个任务的执行情况,执行到哪一步了,每一步的执行结果情况,我们是不知道的。只能等它最终执行完毕后,最后汇总结果。
一个并行框架,它最好是对每一步的执行都能监控。每一步的执行结果,无论成功与失败,它应该有个回调,才算完整。拥有回调的任务,可以监控任务的执行状况,如果执行失败、超时,可以记录异常信息或者处理个性化的默认值。
CompleteableFuture中也有一些回调方法,例如:thenAccept(),whenComplete(),handle(),exceptionally()等,这些方法也能支持任务的回调,但是前提是任务执行了,才能完成回调。在某些场景中,有些任务单元是可能被SKIP跳过不执行的,不执行的任务也应该有回调。
future1.thenCompose(f2,()->xxx)
下游依赖于上游的结果
一组任务,虽然内部的各个执行单元的时间不可控,但是可以控制全组的执行时间不超过某个值。通过设置timeOut,来控制全组的执行阈值。
1 | CompletableFuture.allOf(futures).get(timeout, TimeUnit.MILLISECONDS); |
复用线程
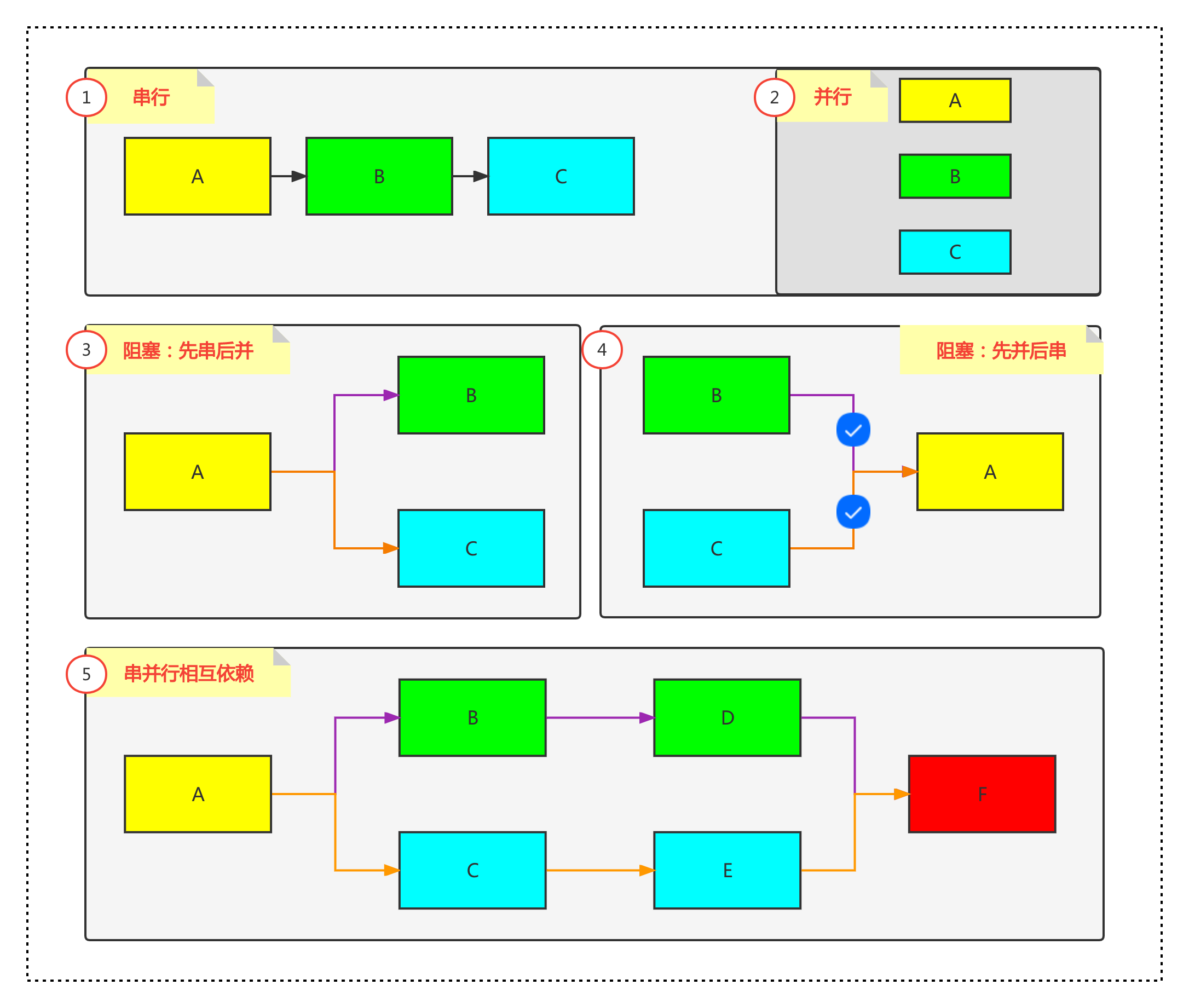
该框架全程无锁,没有一个加锁的地方。
创建线程量少。如上图④中场景。A会运行在B、C执行更慢的那个单元的线程上,而不会额外创建线程。
一个并发框架可能需要具备哪些能力?
1、提供任何形式的串行、并行执行单元的组合
2、为每个执行单元提供执行成功、失败、超时、异常的回调
3、支持为单个执行单元设置异常、失败后的默认值
4、支持为整个group(多个任意组合的执行单元)设置超时时间。单个执行单元失败,不影响其他单元的回调和最终结果获取。如果自己依赖的任务失败,则自己也失败,并返回默认值。
5、整个group执行完毕或超时后,同步阻塞返回所有执行单元结果集,按添加的顺序返回list。也支持整个group的异步回调不阻塞主线程
6、支持每个group独享线程池,或所有group共享线程池(默认)
上面我们总结了多线程的编排场景及实现,以及并发场景的一些潜在需求及实现。
该框架的难点和重点,主要有两点,分别是任务的顺序编排和任务结果的回调。
回调是个很有用的模式,譬如我的主线程执行过程中,要执行一个非常耗时的逻辑。为了不阻塞主线程,自然我们会想到用异步的形式去执行这个耗时逻辑,新建个线程,让这个耗时的逻辑在线程中执行,不阻塞主线程。但问题来了,异步执行没毛病,执行成功、失败后出结果了,该怎么通知主线程?
CompletableFuture提供了许多回调的方法,例如:thenAccept(),whenComplete(),handle(),exceptionally()等。下面列举一些比较常用的回调方法,如下:
1 | //1.计算结果完成,或者异常时执行给定action(当前线程执行) |
CompleteableFuture提供的回调方法,这些方法也能支持任务的回调,但是前提是任务执行了,才能完成回调。在某些场景中,有些任务单元是可能被SKIP跳过不执行的,不执行的任务也应该有回调。
Netty中的回调是非常多的。netty中的future,可以添加Listener,当异步任务执行完毕后,主动回调一下自己就可以了。
整个netty里面大量充斥着类似的回调,但是如果我们要用,仅仅是针对一个或多个异步任务,希望能有个类似的回调,netty就帮不上忙了。
Netty回调的伪代码:其中doSomething是在异步线程里,而回调是在主线程里的。(回调代码是在主线程,回调任务实际是在异步线程里执行的)
1 | //主线程 |
首先我们有这么一个需求,有N个耗时任务,可能是IO任务,我们希望他执行时不会阻塞主线程,而期望它执行完毕(成功\失败)后,来发起一次回调,最好还有超时、异常的回调控制。
我们可以有这样的角色:
1 | package com.soyo.simple; |
作者在issue上推荐一个tomcat只使用一个不定长线程池。
AsyncTool关于多线程并发执行的问题。如果不指定线程池,默认使用不定长线程池。
1 | public static ExecutorService newCachedThreadPool() { |
注意,newCachedThreadPool() 它的核心线程数是0,最大线程数是Integer.MAX_VALUE。可以说它的线程数是可以无限扩大的线程池。
他使用的队列是没有存储空间的,只要请求过来了,如果没有空闲线程,就会创建一个新的线程。
这种不定长线程池,适合处理执行时间比较短的任务。在高并发下,如果在耗时长的RPC\IO操作中使用该线程池,势必会造成系统 线程爆炸。
AsyncTool作者在京东使用的场景多数为低耗时(10ms)高并发,瞬间冲击的场景。这种高并发,且任务耗时较少的,适合使用不定长线程池。
但是这种低耗时的场景也不多,对于耗时较长的场景,推荐使用自定义线程池,可以避免那些耗时长的任务长时间占用线程,造成线程 ”爆炸 “,容错率更高。
总结:
**newCachedThreadPool**** 特性**:核心线程数 0,最大线程数无限,队列无缓存 → 任务一来没线程就新建线程。短耗时 + 高并发场景 → 秒杀下单接口
在这种场景下:
👉 所以 newCachedThreadPool 就特别适合这种“短平快、高并发、瞬时冲击”的场景。
而且双11这种平台肯定是希望用户请求在机器不会崩的情况下流量越多越好,因为下单的单数越多,那么平台赚得越多
两套方案
cluster,sentinel
当发现Redis主节点宕机后,多个sentinel之间会选一个裁判出来,通过投票的方式,多数大于小数,由于这个东西,所以机器数都是基数的,不然就脑裂了
然后再进行从新选主,且由裁判执行
sentinel leader负责选举新的leader,这个过程中还可以挑一个最好的
选择规则:
就是分片,就是分库分表那一套
有个slot的概念,内置了16384个槽,且不能改变。一个slot只能在一台机器上,且在主节点上
crc16(key) % 16384(固定值,不能调节了,所以就不用了 )分配在一个slot上。

resharding
Redis cluster的数据量极限,16384个slot,一个slot一个Redis master节点
1000w * 16384 = 16384000w条数据
PS:俄罗斯人造的东西都有个特点就是快,Nginx也是,走一个极致路线
对比Redis,Redis其实不是纯粹的缓存,自称NOSQL DB,因为可以落盘么
而memcached就是纯粹的缓存
过于简单了,都没自己的命令行工具,直接上去就是开敲
telnet 本地主机 端口
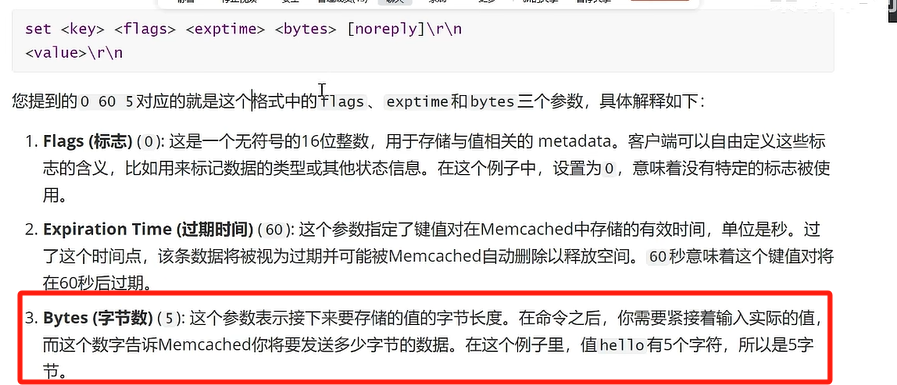
用人来告诉计算机代码更快
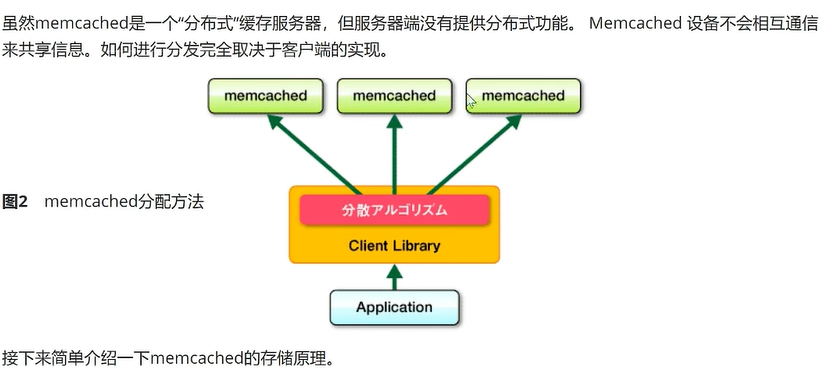
slab allocator,也是池化的思想,不用了还回去,用了再回来

PS:文件真删了,还是能找回来的
原理:
内存结构类似于 快递的蜂巢
画格子
其实就是创建一堆类似不同的数组,内存连续,且内存不会释放,且命令执行多线程,所以才快,
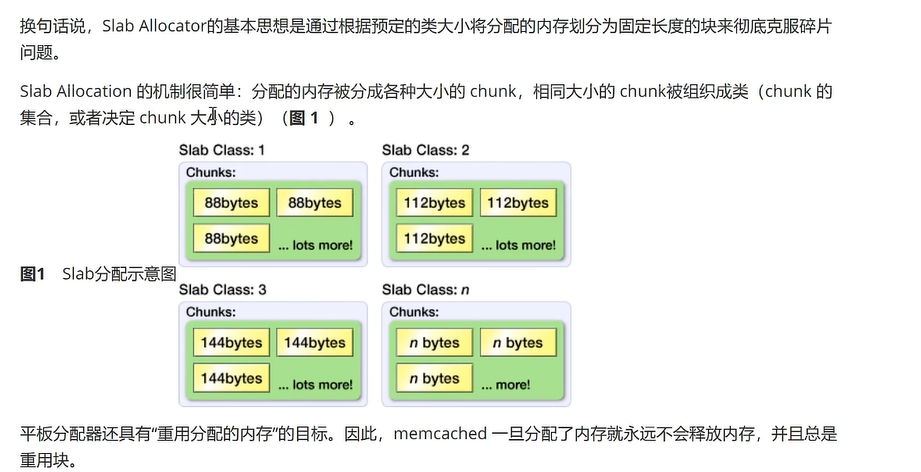
虽然解决了外部碎片,但还是会有内部碎片问题

解决方案:就是重启,凌晨重启
Redis往里加数据,得架构师评省一下,比如加一个set,评故下n,因为那东西是单线程,如果你加的集合后面慢慢变过大的话,是会影响其他的

都是基于set 字符串 get 字符串进行的一个扩展
取模
目的是为了解决传统hash服务上下限导致的hash全都得全部映射好,只需要部分改变,比如k1推到s1,但s1没了,只会影响k1,而不会影响到其他
以及可以让同一类请求每次都映射到同一节点上,适用于 本地缓存之类的场景,提高缓存命中率
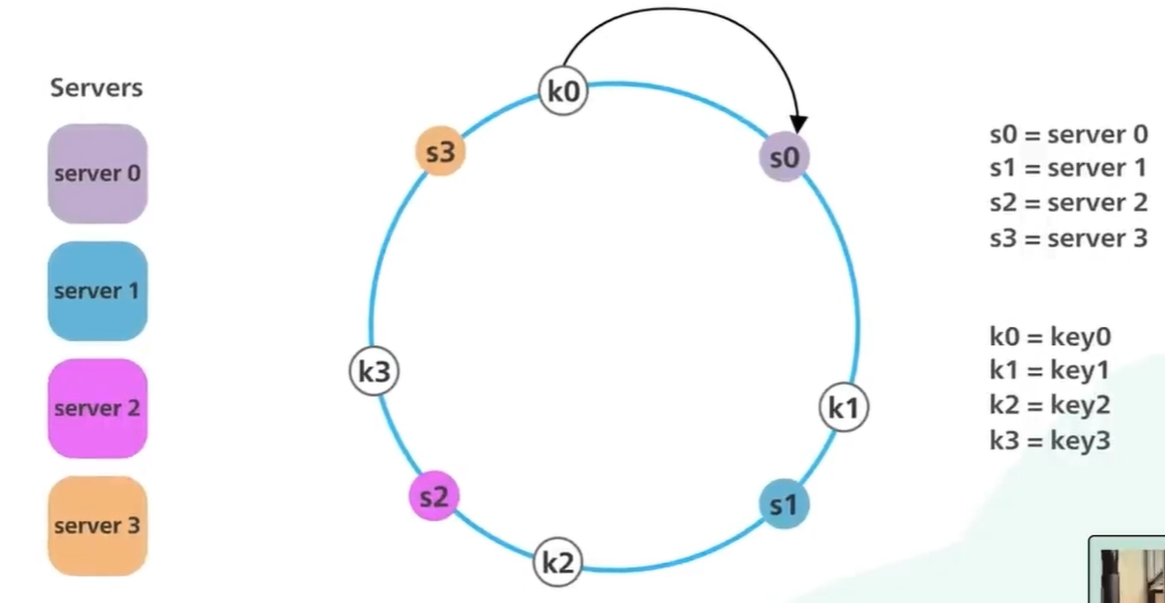
虚拟节点解决的问题:实例节点分布不均
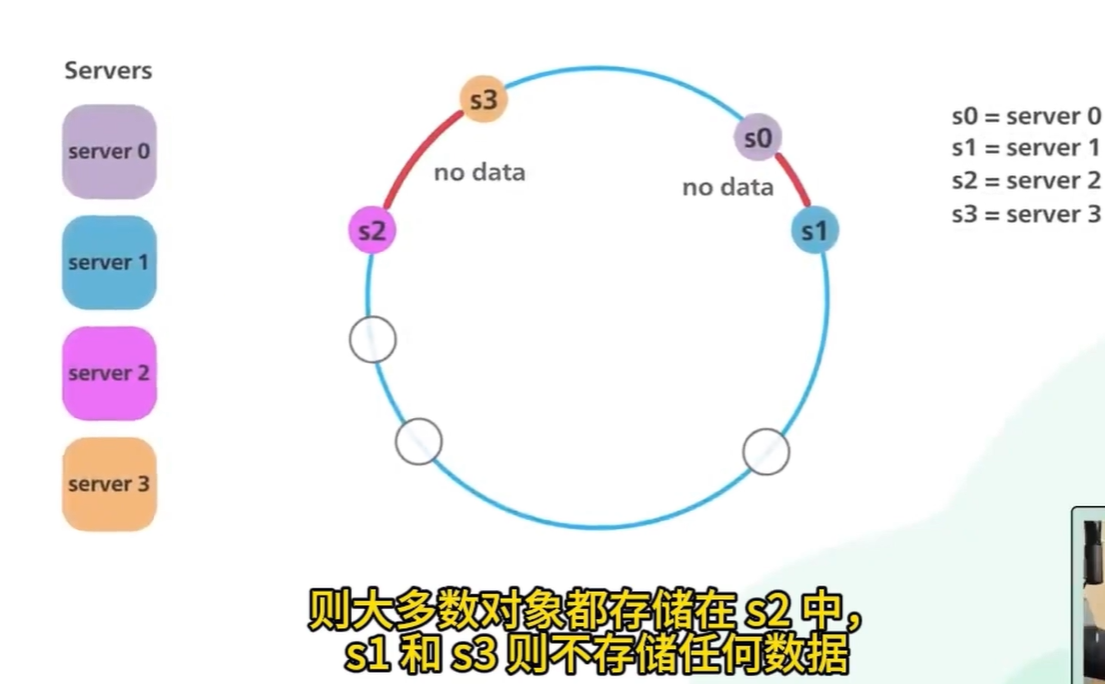
虚拟节点越多,hash上的对象分配更均匀
1 | package com.grace.gateway.core.algorithm; |
1 | @Override |
单调栈分为单调递增,单调递减
👉 核心模式就是:
1 | for (...) { |
题目:找出每个元素多少index后会出现比他大的元素
思路:
1 | class Solution { |
时间复杂度:ON
空间复杂度:ON
思路:
1 | class Solution { |
思路:
1 | class Solution { |
1 | class Solution { |
题目:
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润
思路:
1 | class Solution { |
1 | class Solution { |
思路:DP,四部曲 ,数组含义,初始化,状态,推导
1 | class Solution { |
思路:
1 | class Solution { |
思路:
1 | class Solution { |
1 | class Solution { |
思路:动态规划
就嗯记,dp思路 相邻三个矩形边长的最小值+1
dp数组含义即 以matrix[i][j] 为右下角为右下角的最大正方形边长
1 | class Solution { |
思路:
1 | class Solution { |
输出路径
1 | class Solution { |
思路:
1 | class Solution { |
https://chatgpt.com/s/t_68ea8e7831c48191ba35865a1392cdee
思路

1 | class Solution { |
压缩:
1 | class Solution { |
分割成和最相近的两个子集
完全背包
1 | class Solution { |
1 |
思路
1 | /** |
思路
1 | class Solution { |
思路
1 |
|
SQL题
codetop刷题
实习产出
项目
场景题(开放式数据量级问题)
手写系列
卷叶卷到死。。