排序

发表于 更新于 分类于 阅读次数：

排序数组[321]

思路

快排，堆，计数，归并

  1. 快排
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
    public static Random random = new Random();
    public int[] sortArray(int[] nums) {
        sort(nums, 0, nums.length - 1);
        return nums;
    }
    public void sort(int []nums, int l, int r){
        if( l >= r) return;

       int indexX = partition(nums, l, r);
       //l....indexX
       sort(nums, l ,indexX - 1);
       //indeX...r
       sort(nums, indexX + 1, r);
    }
    public int partition(int []nums, int l, int r){
        int i = l + random.nextInt( r - l + 1);
        int x = nums[i];
        swap(nums, l, i);
        int curL = l + 1;
        int curR = r;
        while(true){
            while(curL <= curR && nums[curL] < x){
                curL++;
            }
            while(curL <= curR && nums[curR] > x){
                curR--;
            }
            if(curL >= curR) break;

            swap(nums, curL, curR);
            curL++;
            curR--;
        }
        swap(nums, l, curR);

        return curR;
    }
    public void swap(int []nums, int i, int j){
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}
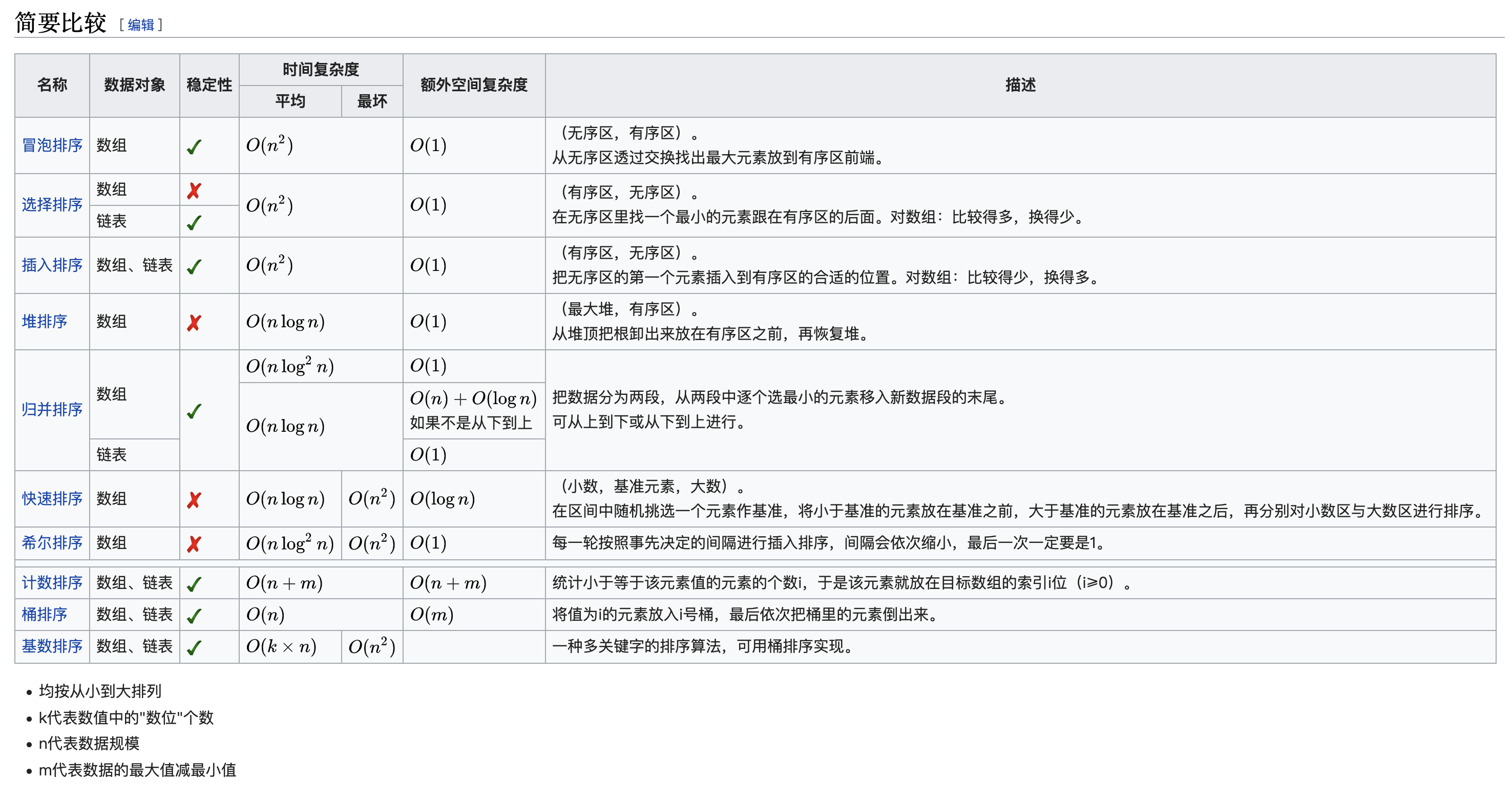
  1. 题目特殊性，时间复杂度为O(N)的解法，采用计数排序

https://leetcode.cn/problems/sort-an-array/solutions/179210/dang-wo-tan-pai-xu-shi-wo-zai-tan-xie-shi-yao-by-s/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution {
    public int[] sortArray(int[] nums) {
        int max = 50001;
        int min = -50001;

        int[] counter = new int[max - min + 1];
        for (int num : nums) {
            counter[num - min]++;
        }
        int index = 0;
        //index 为 数组值 value为 数组值的个数
        for (int i = min; i <= max; i++) {
            int cnt = counter[i - min];
            // cnt > 0说明存在
            while (cnt > 0) {
                nums[index] = i;
                cnt--;
                index++;
            }
        }
        return nums;
    }
}

  1. 归并排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
class Solution {
    public int[] sortArray(int[] nums) {
        sort(nums, 0, nums.length - 1);
        return nums;
    }
    //归并排序
    public void sort(int []nums, int l, int r){
        if(l >= r) return;
        int mid = l + (r - l) / 2;
        sort(nums, l, mid);
        sort(nums, mid + 1, r);
        //合并 [l...mid] [mid + 1....r]
        merge(nums, l, mid, mid + 1, r);
    }
    public void merge(int []nums, int s1, int e1, int s2, int e2){
        // [s1...e1] [s1 ... e2]
        int i = s1;
        int j = s2;
        // [2,4] [1,5]
        // [1,2,4,]
        int []temp = new int[e2 - s1 + 1];
        int n = temp.length;
        int k = 0;
        while(i <= e1 || j <= e2){
            while( i > e1 && j <= e2){
                temp[k] = nums[j];
                k++;
                j++;
            }
            while(j > e2 && i <= e1){
                temp[k] = nums[i];
                k++;
                i++;
            }
            if(k >= n) break;
            //谁小谁先移动
            if(nums[i] > nums[j]){
                temp[k] = nums[j];
                k++;
                j++;
            }
            else {
                temp[k] = nums[i];
                k++;
                i++;
            }
        }
        System.arraycopy(temp, 0, nums, s1, temp.length);
        
    }
    public void swap(int[] nums, int i, int j){
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

字典序排数[13]

思路：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public List<Integer> lexicalOrder(int n) {
        //256
        // 1 10 100 101...109 11
        List<Integer> res = new ArrayList();
        for (int i = 0, j = 1; i < n; i++) {
            res.add(j);
            if (j * 10 <= n) {
                j = j * 10;
            } else {
                // 1 10 100 101...109 11 or  1,2 
                // 109 -> 11 ,2 -> 3
                while (j % 10 == 9 || j + 1 > n) {
                    j = j / 10;
                }
                j++;
            }
        }
        return res;
    }
}

排序链表[133]

思路：

  1. 归并排序
    head….tail-> head….mid mid…tail

不断分，然后并起来

归：对链表进行分割，直到每个链表只有一个 元素

并：对链表进行升序合并

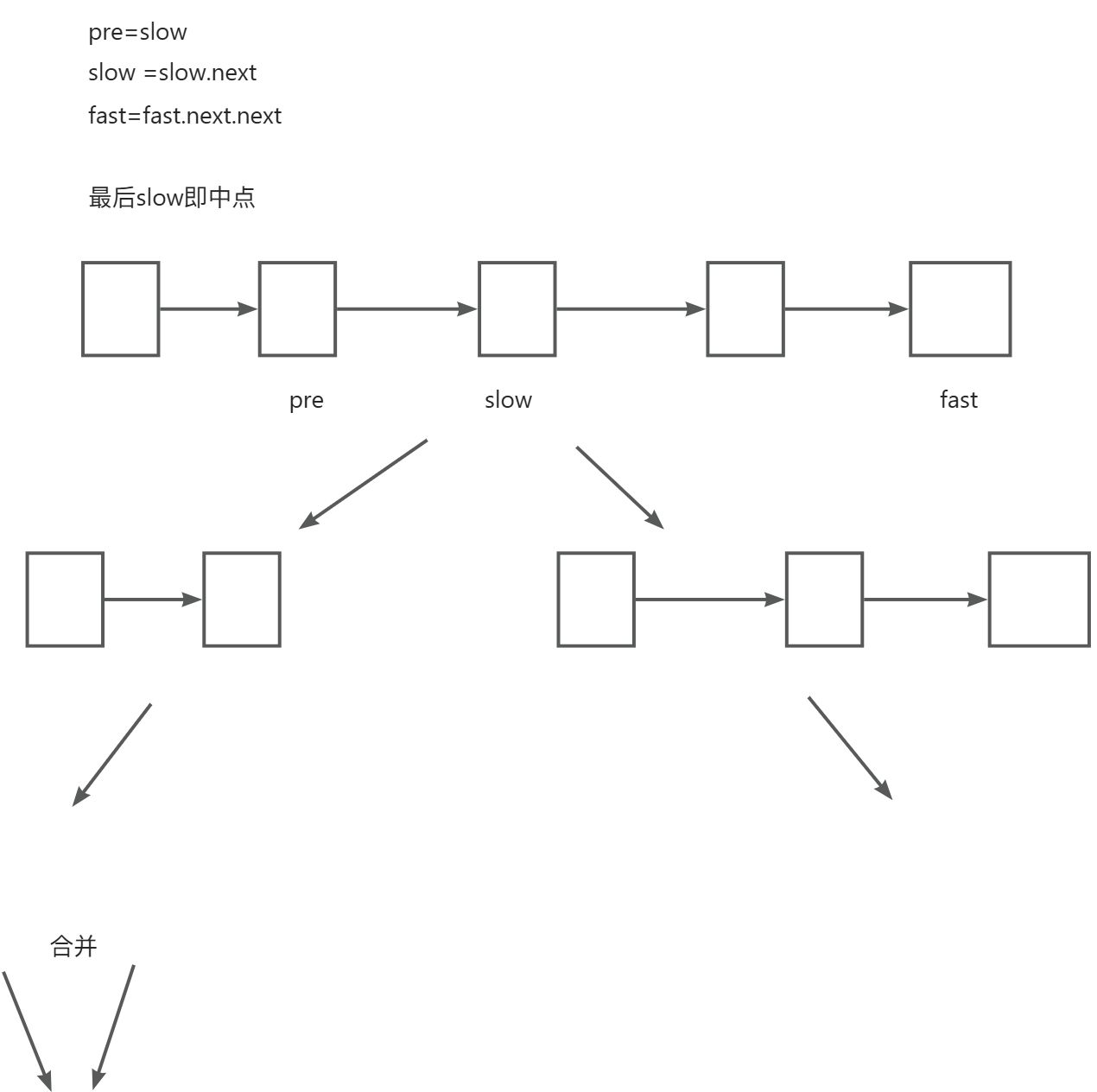
链表取中点（快慢指针），并切割

  1. 快排（容易超时）

图（归并）

画板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode sortList(ListNode head) {
        return sort(head);
    }

    //从中间分开
    public ListNode divide(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        ListNode pre = head;
        while (fast != null && fast.next != null) {
            pre = slow;
            fast = fast.next.next;
            slow = slow.next;
        }
        pre.next = null;
        return slow;
    }

    //归并排序
    public ListNode sort(ListNode head1) {
        if (head1 == null || head1.next == null) {
            return head1;
        }
        //拆成两部分，并返回后部门的头结点
        ListNode head2 = divide(head1);
        //mid(4→2→1→3)   ---> 分成两部分
        //head1: 4 → 2 → null
        //head2: 1 → 3 → null
        head1 = sort(head1);

        head2 = sort(head2);

        return merge(head1, head2);
    }

    //两链表合并，要有序
    // head1 .... 
    // head2 ....
    public ListNode merge(ListNode head1, ListNode head2) {
        ListNode res = new ListNode();
        ListNode cur = res;
        while (head1 != null || head2 != null) {
            if (head2 == null) {
                cur.next = head1;
                break;
            }
            if (head1 == null) {
                cur.next = head2;
                break;
            }
            if (head1.val > head2.val) {
                cur.next = head2;
                head2 = head2.next;
            } else {
                cur.next = head1;
                head1 = head1.next;
            }
            cur = cur.next;
        }
        return res.next;
    }
}

时间复杂度：NlogN 空间复杂度：logN

合并K个排序链表[221]

思路：

  1. 归并排序
  2. 堆（可能需要手写）排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        if(lists.length == 0) return null;
        //最小堆，堆顶为最小值
        PriorityQueue<ListNode> pq = new PriorityQueue<>((a, b) -> a.val - b.val);
        //先将最小的放进来
        for(ListNode head: lists){
            if(head == null) continue;
            pq.add(head);
        }
        ListNode dummyHead = new ListNode();
        ListNode res = dummyHead;
        
        while(!pq.isEmpty()){
            ListNode minNode = pq.poll();
            res.next = minNode;
            res = res.next;
            if(minNode.next != null){
                pq.add(minNode.next);
            }
        }
        return dummyHead.next;
    }
}
  • 时间复杂度：O(Llogm)，其中 m 为 lists 的长度，L 为所有链表的长度之和。

数组中的第K个最大元素[550]

题目：

  1. 要求时间复杂度为O(N)

思路：

  1. 维护size == k的最小堆（但不符合题意）时间复杂度：nums.length log(k)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int findKthLargest(int[] nums, int k) {
        if(nums.length == 1) return nums[0];
        PriorityQueue<Integer> pq = new PriorityQueue();
        for(int i: nums){
            pq.add(i);
            if(pq.size() > k){
                pq.poll();
            }
        }
        //System.out.println(pq);
        return pq.isEmpty()?-1:pq.poll();
    }
}
  1. 快速选择

思路：

  1. 构建partition函数，里面干的就是 数组随机取一个 x，然后划分 x
  2. 如何划分！？
    1、小技巧，先将 l 和 x交换，方便后面处理

2、curL–> …. <—curR，while把curL和curR推进到需要交换的位置，然后swap，交换后，重复这个过程
外层while(true) 内层while 推进curL,curR。若curR<=curL退出全部循环

3、将x放回正确位置，—> swap(l,curR)

  1. 经过划分我们可以得到x。那么这个时候判断x的index 和 targetIndex( n - k)的位置
  2. 若 index = targertIdex 就是找到答案了，直接返回。若index > targetIndex 则说明targetIndex在右边，那么这个时候让r = index缩小范围，反之，让l = index
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
class Solution {
    private static final Random rand = new Random();

    public int findKthLargest(int[] nums, int k) {
        //选一个基准 元素 x
        // <x.... x... >x
        //如果 i = n - k ,那么 res = i
        //如果 i > n - k, 那么res在左侧，我们在其中寻找，重复第一步
        //如果 i < n - k, 那么res在右侧，我们在其中寻找，重复第一步
        if(nums.length < k) return -1;
        int n = nums.length;
        int l = 0;
        int r = n - 1;
        int targetIndex = n - k;
        while(true){
            int resIndex = partition(nums, l, r);
            if(resIndex == targetIndex){
                return nums[resIndex];
            }
            //redIndex 在 targetIndex右边 说明 targetIndex的数在 l...resIndex 中
            else if(resIndex > targetIndex){
                r = resIndex - 1;
            }
            else {
                l = resIndex + 1;
            }
        }
    }
    public int partition(int []nums, int l, int r){
        int i = l + rand.nextInt(r - l + 1);
        int x = nums[i];
        //System.out.println(x); 
        //交换左边界元素 和 x，方便后面实现
        swap(nums, l, i);
        //System.out.println(Arrays.toString(nums));
        int curL = l + 1;
        int curR = r;
        //处理示意图： (< x) curL-> (没处理的元素) <-curR ( > x)
        while(true){
            while(curL <= curR && nums[curL] < x){
                curL++;
            }
            //经过上面的while循环此时 nums[curL] >= x
            while(curL <= curR && nums[curR] > x){
                curR--;
            }
            //经过上面的while循环此时 nums[curL] <= x
            if(curL >= curR) break;
            swap(nums, curL, curR);
            curR--;
            curL++;
        }

        //System.out.println(Arrays.toString(nums)); 
        swap(nums, l, curR);
        //System.out.println(Arrays.toString(nums)); 
        return curR;
    }
        // 交换 nums[i] 与 nums[j]
    private void swap(int[] nums, int i, int j) {
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

颜色分类[41]

思路：

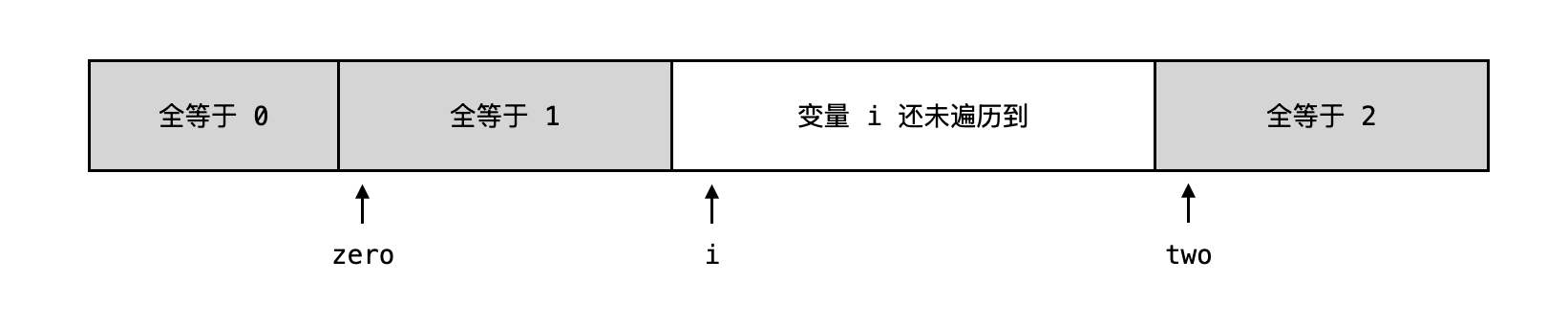
  1. 三路快排（三指针法）。0…zero i two…n -1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35


class Solution {
    public void sortColors(int[] nums) {
        int n = nums.length;
        
         
        int i = 0;
        int zero = 0;
        int two = n - 1;
        //[0 zero] 全为 0 
        //[zero i] 全为 1
        //[two, n-1] 全为 2
        // 0 1 2
        while(i <= two){
            if(nums[i] == 0){
                swap(nums, i, zero);
                zero++;
                i++;
            }
            else if(nums[i] == 1){
                i++;
            }
            else {
                swap(nums, i, two);
                two--;
            }
        }
    }
    public void swap(int[] nums, int i, int j){
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

或者计数排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public void sortColors(int[] nums) {
        int[] counter = new int[3];
        for(int i: nums){
            counter[i]++;
        }
        int index = 0;
        for(int i = 0; i < 3; i++){
            int cnt = counter[i];
            while(cnt > 0) {
                nums[index] = i;
                index++;
                cnt--;
            }
        }
    }
}