dfs

必看

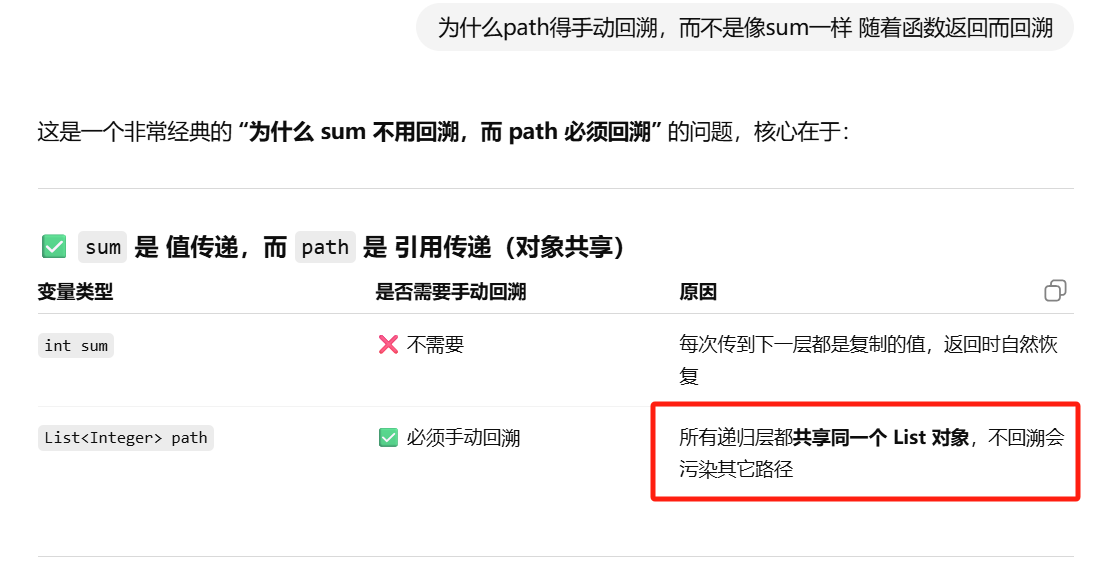
回溯模版的解释

//向数组中的每个整数前添加 '+' 或 '-'

//对于每个节点两种选择： + or -。不能硬套模版
/**
fun dfs():
    for(int i = 0; i < nums.length; i++){
        add
        dfs
        delete
    }
以上是因为每个节点都有多选择 比如 排列，组合


 */

岛屿数量[289]

思路：

1.

class Solution {
    int [][]direct={{1,0},{0,1},{-1,0},{0,-1}};
    public int numIslands(char[][] grid) {
        int res=0;
        for(int i=0;i<grid.length;i++){
            for(int j=0;j<grid[0].length;j++){
                if(grid[i][j]=='1'){
                  res++;
                  dfs(grid,i,j);
                }
            }
        }
        return res;
    }
    public void dfs(char [][]grid,int x,int y){
        if(x<0||y<0||x>=grid.length||y>=grid[0].length){
           return;
        }
        if(grid[x][y]=='0'){
           return;
        }
        else {
            //用海水把陆地淹掉，相当于valid数组的作用
            grid[x][y]='0';
        }
        for(int i=0;i<4;i++){
           //四个方向
           int nextX=x+direct[i][0];
           int nextY=y+direct[i][1];
           dfs(grid,nextX,nextY);
        }
    }
}

@週刊少年 时间复杂度BFS会低一点，空间复杂度感觉DFS会好一点（但是要考虑递归调用的堆栈的空间就不好说了）

被问到深度优先和广度优先的差别、计算时间空间复杂度
面试用BFS写出来了，然后让我用并查集再写一个，字节

全排列[277]

思路：

1. used[i] 用于控制 防止走回头路

class Solution {
    List<List<Integer>> res=new ArrayList<>();
    //存放路径
    List<Integer> path=new ArrayList<>();
    public List<List<Integer>> permute(int[] nums) {
        boolean []used=new boolean[nums.length];
        dfs(nums,used);
        return res;
    }
    public void dfs(int []nums,boolean []used){
        if(path.size()==nums.length){
          res.add(new ArrayList<>(path));
        }
        for(int i=0;i<nums.length;i++){
           if(used[i]){
              continue;
           }
           //递归
           path.add(nums[i]);
           used[i]=true;
           dfs(nums,used);
           //回溯
           path.removeLast();
           used[i]=false;
        }
    }
}

时间复杂度：

问题类型	是否需要 startIndex	控制逻辑	示例
排列 Permutation	❌ 不需要	用 used[i] 防止重复选	[1,2] vs [2,1] 都算不同
组合 Combination	✅ 必须	用 startIndex 防止重复，为了防止来回选，必须 保证后面的选择只能从当前元素后面开始。	[1,2] 和 [2,1] 视为相同

全排列 II[57]

去重版的全排列 I，用HashSet存结果集即可

课程表[56]

思路：

1. spring

class Solution {
    //k：
    Map<Integer, List<Integer>> graph = new HashMap<>();
    Set<Integer> wait = new HashSet<>();      // 当前正在修的课程（类似 wait 集合）
    Set<Integer> completed = new HashSet<>(); // 已确认可修完的课程（类似缓存）

    public boolean canFinish(int numCourses, int[][] prerequisites) {
        // 构建依赖图
        for(int i=0;i<numCourses;i++) graph.put(i, new ArrayList<>());
        for(int[] pre : prerequisites) graph.get(pre[1]).add(pre[0]);

        // 遍历所有课程
        for(int i=0;i<numCourses;i++)
            if(!completed.contains(i) && !dfs(i)) return false;

        return true;
    }

    private boolean dfs(int course) {
        if(wait.contains(course)) return false; // 当前路径已出现 → 有环
        if(completed.contains(course)) return true; // 已确认可完成

        wait.add(course); // 加入 wait 集合（正在修）
        for(int next : graph.get(course)) {
            if(!dfs(next)) return false; // 依赖课程不可修完 → 当前也不可修
        }
        wait.remove(course);       // 移出 wait 集合
        completed.add(course);     // 加入已完成缓存
        return true;
    }
}

交错字符串[27]

单词拆分[64]

思路：

DFS + 记忆化搜索

还是得把回溯树给画出来，才清晰易懂！！！（明天来搞）

https://leetcode.cn/problems/word-break/solutions/302779/shou-hui-tu-jie-san-chong-fang-fa-dfs-bfs-dong-tai/

竟然可以记忆化，说明可以转成DP

判断可能性大概率是 DP

class Solution {
    Boolean []memory ;
    public boolean wordBreak(String s, List<String> wordDict) {
        memory = new Boolean[s.length()];
        return dfs(s, 0, wordDict);
    }
    //leetcode7
    //leet code 
    public boolean dfs(String s,int startIndex,List<String> wordDict){
        if(startIndex == s.length()) return true;
        if(memory[startIndex] != null){
            return memory[startIndex];
        }
        for(String word: wordDict){
            int nextStartIndex = startIndex + word.length();
            if(nextStartIndex > s.length()){
                continue;
            }
            //startsWith：s中startIndex开头的子串是否以word开头
            if(s.startsWith(word, startIndex) && dfs(s,nextStartIndex,wordDict)){
                memory[startIndex] = true;
                return true;
            }
        }
        memory[startIndex] = false;
        return false;
    }
}

电话号码的字母组合[19]

思路：

1. 回溯，最基础的题了。可以细想一下这个递归，最容易的一次

[abc]

[iop]
交叉相乘，笛卡尔集

排列何尝不是一种算 笛卡尔集合
[a b c]
[a b c]
[a b c]
abb 只不过递归的集合不断为自己本身

for (int i = 0; i < t.get(tIndex).length(); i++) {
    path.append(t.get(tIndex).charAt(i));
    dfs(tIndex + 1);
    path.deleteCharAt(path.length() - 1);
}

class Solution {
    Map<Integer, String> map = new HashMap();
    List<String> t = new ArrayList();
    List<String> res = new ArrayList();
    StringBuilder path = new StringBuilder();

    public List<String> letterCombinations(String digits) {
        map.put(1, "");
        map.put(2, "abc");
        map.put(3, "def");
        map.put(4, "ghi");
        map.put(5, "jkl");
        map.put(6, "mno");
        map.put(7, "pqrs");
        map.put(8, "tuv");
        map.put(9, "wxyz");

        for (char c : digits.toCharArray()) {
            t.add(map.get(c - '0'));
        }
        dfs(0);
        return res;
    }

    public void dfs(int tIndex) {
        if (path.length() == t.size()) {
            res.add(path.toString());
            return;
        }
        for (int i = 0; i < t.get(tIndex).length(); i++) {
            path.append(t.get(tIndex).charAt(i));
            dfs(tIndex + 1);
            path.deleteCharAt(path.length() - 1);
        }
    }
}

删除无效的括号[18]

思路

1. 将左右括号 -+化
2. 对于path，则在参数中update

class Solution {
    Set<String> res = new HashSet();
    int max = 0;
    String s;
    int n;
    //最大路径长度
    int maxPathLen = 0;
    public List<String> removeInvalidParentheses(String _s) {
        //左右括号
        int l = 0;
        int r = 0;
        s = _s;
        n = s.length();
        for(char c: s.toCharArray()){
            if(c == '(') l++;
            else if(c == ')') r++;
        }
        //max：最大括号数（单括号）
        max = Math.max(l, r);
        dfs(0, "", 0);
        return new ArrayList(res);
    }
    /**
     * 遍历 _s 字符串，记录有效路径
     * @param curCharIndex 当前遍历的字符下标
     * @param path 遍历时的路径（括号组合字符串）
     * @param score 分数，用于标记左右括号的得分，左则+1，右则-1
     */
    public void dfs(int curCharIndex, String path, int score){
        //不合法情况，0 <= score <= max 
        if(score < 0 || score > max) return;
        
        //当下标等于字符串长度，即遍历完时，则说明搜索完成，保存合法结果到 set
        if(curCharIndex == n){
            //只有score == 0结果才合法，并且当前路径长度要大于最大路径子串的长度才记录或者更新
            //小于最长路径子串就不用更新了
            if(score == 0 && path.length() >= maxPathLen){
                //为什么要有这一步，因为题目要求 删除最小数量的无效括号，换句话说，就是你结果集里的合法字符串要为最长的
                //如果有更长的了，就把前面的clear掉
                if(path.length() > maxPathLen) res.clear();
                
                //更新最大路径子串
                maxPathLen = path.length();
                res.add(path);
            }
            return;
        }
        //当前字符
        char c = s.charAt(curCharIndex);
        
        //对于( ) 都有选和不选两种选择
        if(c == '('){ // 选左括号，score + 1；不选score不变
            dfs(curCharIndex + 1, path + c, score + 1);
            dfs(curCharIndex + 1, path, score);
        }
        else if(c == ')'){// 选左括号，score - 1；不选score不变
            dfs(curCharIndex + 1, path + c, score - 1);
            dfs(curCharIndex + 1, path, score);
        }//选正确字符不变
        else dfs(curCharIndex + 1, path + c, score);
    }
}

戳气球

思路

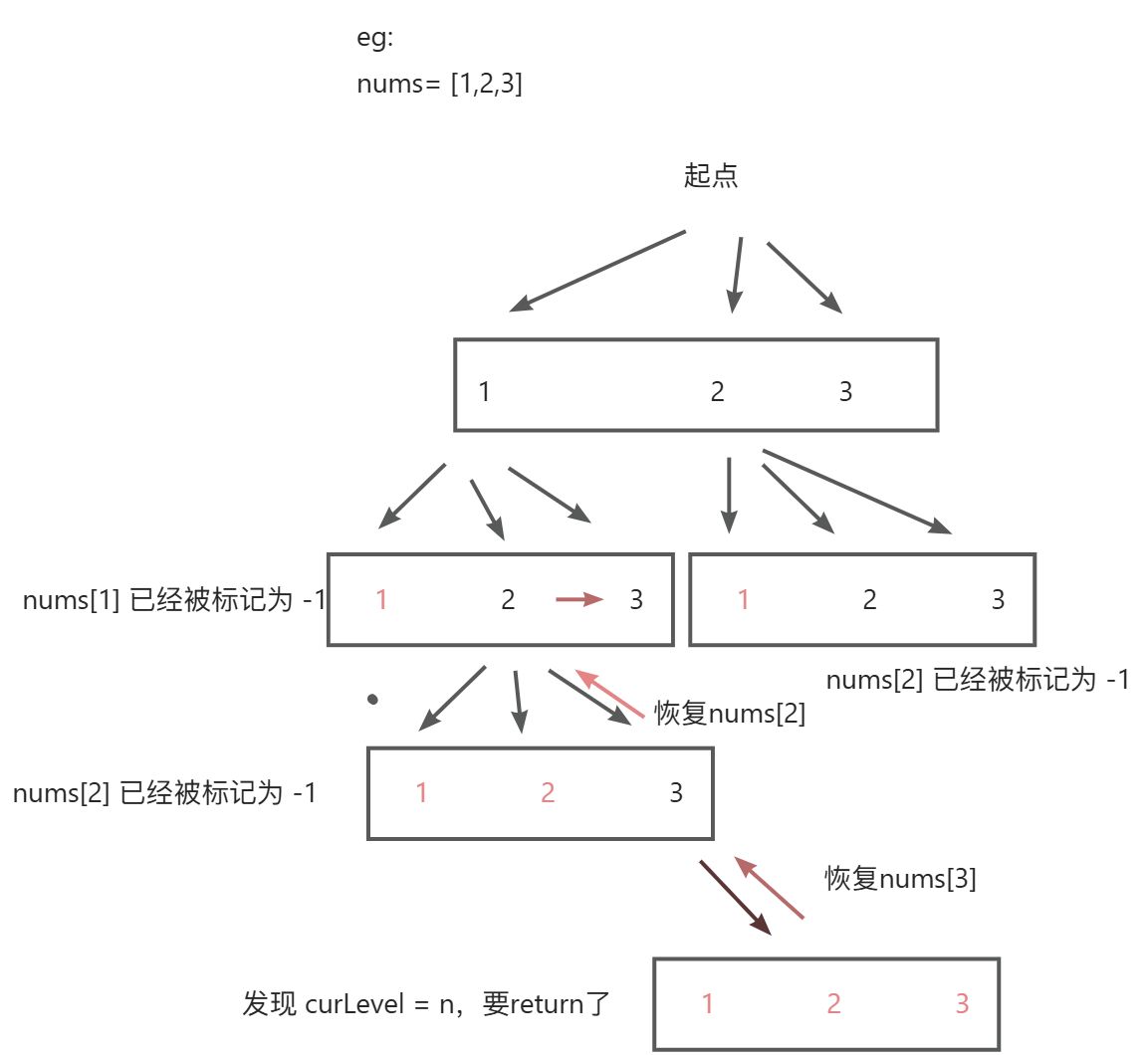
1. dfs + 回溯，有一个n层的数组，然后我往下走，戳当前i节点，并在下次递归之前把当前节点置为 -1，防止重复选，curLevel == n时更新结果。但超时，得进行记忆化

回溯树：

class Solution {
    int n;
    int res = 0;
    public int maxCoins(int[] nums) {
        n = nums.length;
        dfs(nums, 0, 0);
        return res;
    }
    public void dfs(int[] nums, int curLevel, int curCoin){
        //回溯：一个n层的数组，我们从第一层走到底n层
        //nums[i] = -1来防止 重复选
        //为什么不是startIndex，这个主要是决定 选元素只能从startINdex后开始选，而不能往回选，对于组合这种 1 2和 2 1是一样的
        if(curLevel == n){
            res = Math.max(res, curCoin);
            return;
        }
        for(int i = 0; i < nums.length; i++){
            if(nums[i] == -1){
                continue;
            }
            int midQ = nums[i];
            //左测的气球编号
            int lQ = 1;
            //右侧的气球编号
            int rQ = 1;
            int l = i - 1;
            int r = i + 1;
            while(l >= 0 && nums[l] == -1){
                l--;
            }
            if(l < 0) lQ = 1;
            else lQ = nums[l];
            while(r < nums.length && nums[r] == -1){
                r++;
            }
            if(r >= nums.length) rQ = 1;
            else rQ = nums[r];
            int add = lQ * midQ * rQ;
            nums[i] = -1;

            //右侧的气球
            dfs(nums, curLevel + 1, curCoin + add);
            nums[i] = midQ;
        }
    }
}

时间复杂度 = O(n! × n)

2. dp，dp[i][j] 表示 i 到 j能获得的最大金币
3. dp[i][j] = 区间内的最大。那么dp[i][i + len] = res;

class Solution {
    public int maxCoins(int[] nums) {
        int n = nums.length;
        // 创建一个辅助数组，并在首尾各添加1，方便处理边界情况
        int[] temp = new int[n+2];
        temp[0] = 1;
        temp[n+1] = 1;
        for(int i=0; i<n; i++){
            temp[i+1] = nums[i];
        }
        int[][] dp = new int[n+2][n+2];
        // len表示开区间长度
        for(int len=3; len<=n+2; len++){
            // i表示开区间左端点
            for(int i=0; i<=n+2-len; i++){
                int res = 0; 
                // k为开区间内的索引
                for(int k = i+1; k<i+len-1; k++){
                    int left = dp[i][k];
                    int right = dp[k][i+len-1];
                    //dp[i][j] 表示 i 到 j能获得的最大金币
                    //(i....k) k (k.... i + len -1)
                    res = Math.max(res, left + temp[i]*temp[k]*temp[i+len-1] + right);
                }
                dp[i][i+len-1] = res;
            }
        }
        return dp[0][n+1];
    }
}

目标和[22]

思路

1. DFS
2. 每个节点两种选择 + or -

比较简单的回溯，和普通的回溯的区别，就是在循环过程中，如果是像组合排列这些题，就需要往后遍历找，即树的宽度不定，而这题则树宽为 1，每次直接一个数递归下去即可，不用循环。

class Solution {
    int res = 0;
    public int findTargetSumWays(int[] nums, int target) {

        dfs(nums, target, 0, 0);
        return res;
    }
    public void dfs(int[] nums, int target, int numIndex, int sum){
        if(numIndex == nums.length){
            if(target == sum) res++;
            return ;
        }
        //向数组中的每个整数前添加 '+' 或 '-'

        //对于每个节点两种选择： + or -。不能硬套模版
        /**
        fun dfs():
            for(int i = 0; i < nums.length; i++){
                add
                dfs
                delete
            }
        以上是因为每个节点都有多选择 比如 排列，组合
        
        
         */
        dfs(nums, target, numIndex + 1, sum + nums[numIndex]);
        dfs(nums, target, numIndex + 1, sum - nums[numIndex]);
    }
}

路径总和 II[75]

题目：

求叶子节点到根节点 路径和 为target的路径

思路：

1. dfs 回溯。
2. 注意！！！ 叶子结点定义，root.left == null && root.right == null

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    List<List<Integer>> res = new ArrayList();

    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        if(root == null) return new ArrayList(res);
        dfs(root, targetSum, 0, new ArrayList());
        return res;
    }

    public void dfs(TreeNode root, int targetSum, int sum, List<Integer> path) {
        if (root == null) {
            // if (sum == targetSum)
            //     // res.add(path.chars()
            //     //         .map(e -> e - '0')
            //     //         .boxed()
            //     //         .collect(Collectors.toList()));
            //     res.add(new ArrayList(path));
            // return;
            return ;
        }

        sum += root.val;
        //System.out.println(sum);
        path.add(root.val);
        //System.out.println(path);

        //到达叶子节点
        if(root.left == null && root.right == null){
            if (sum == targetSum)
                res.add(new ArrayList(path));
            //return; 肯定不能return啊，因为它是叶子结点到根节点
        }
        dfs(root.left, targetSum, sum, path);
        dfs(root.right, targetSum, sum, path);
        //回溯
        path.remove(path.size() - 1);
    }
}