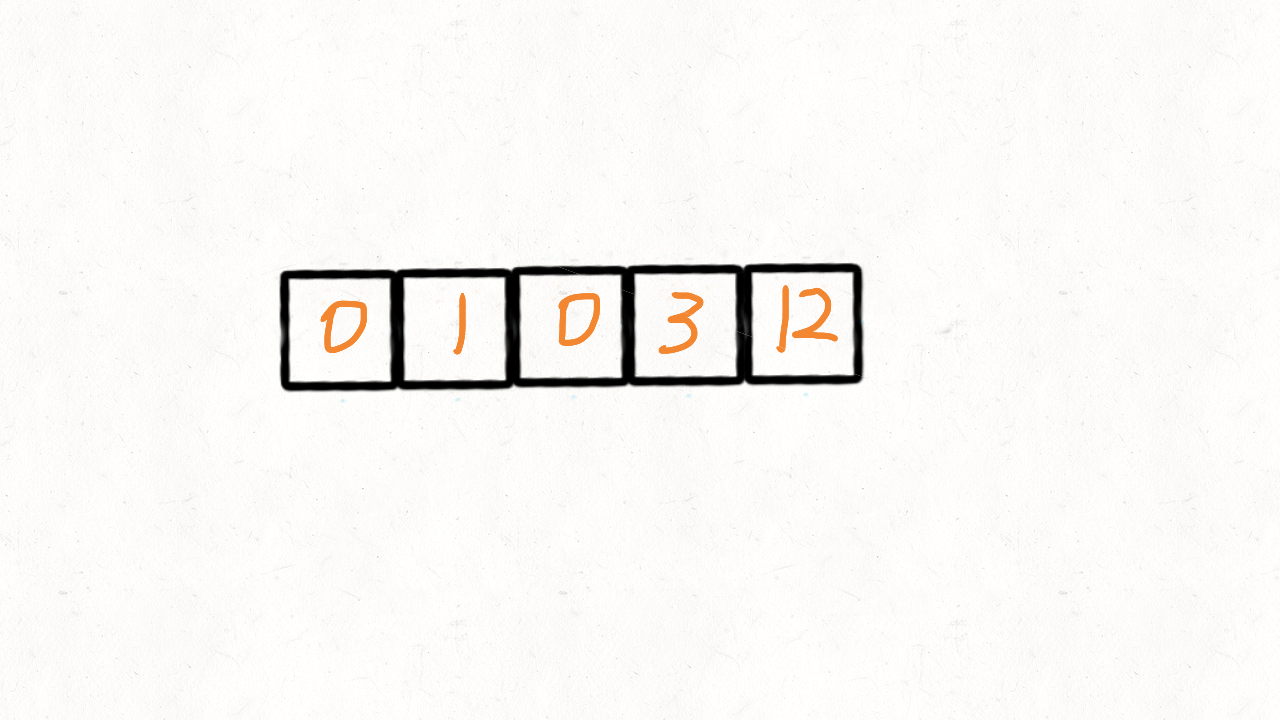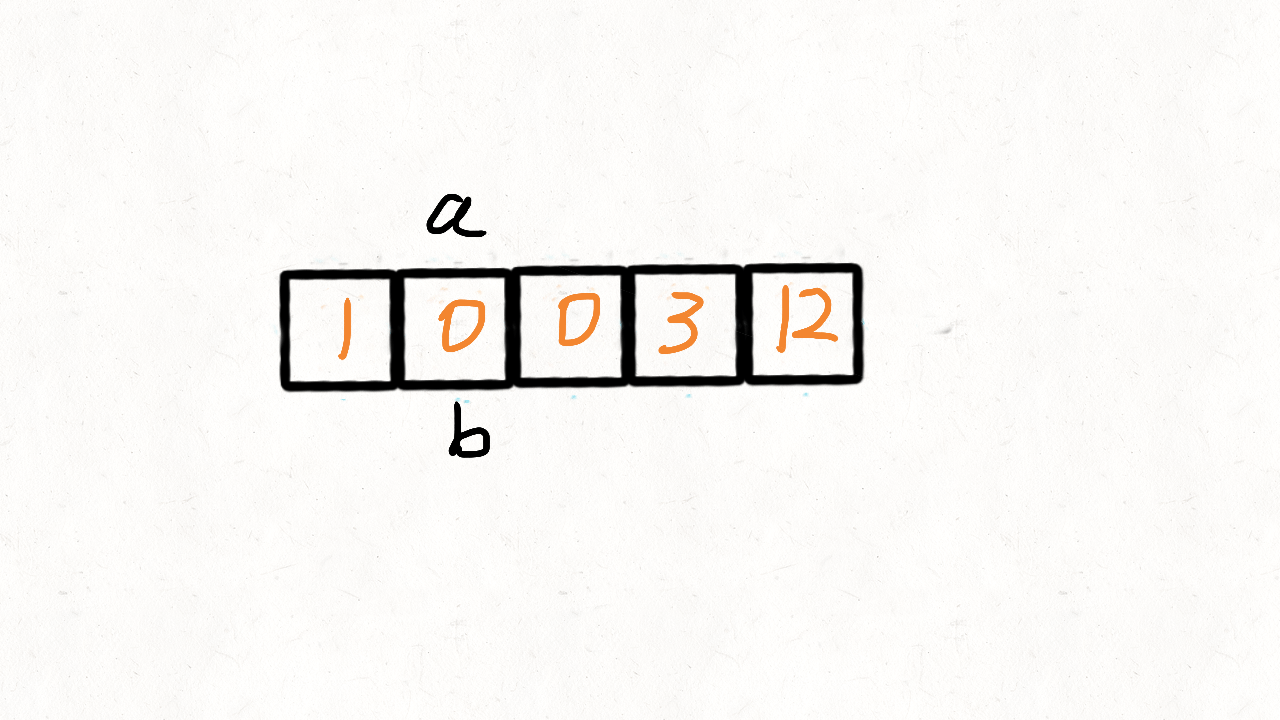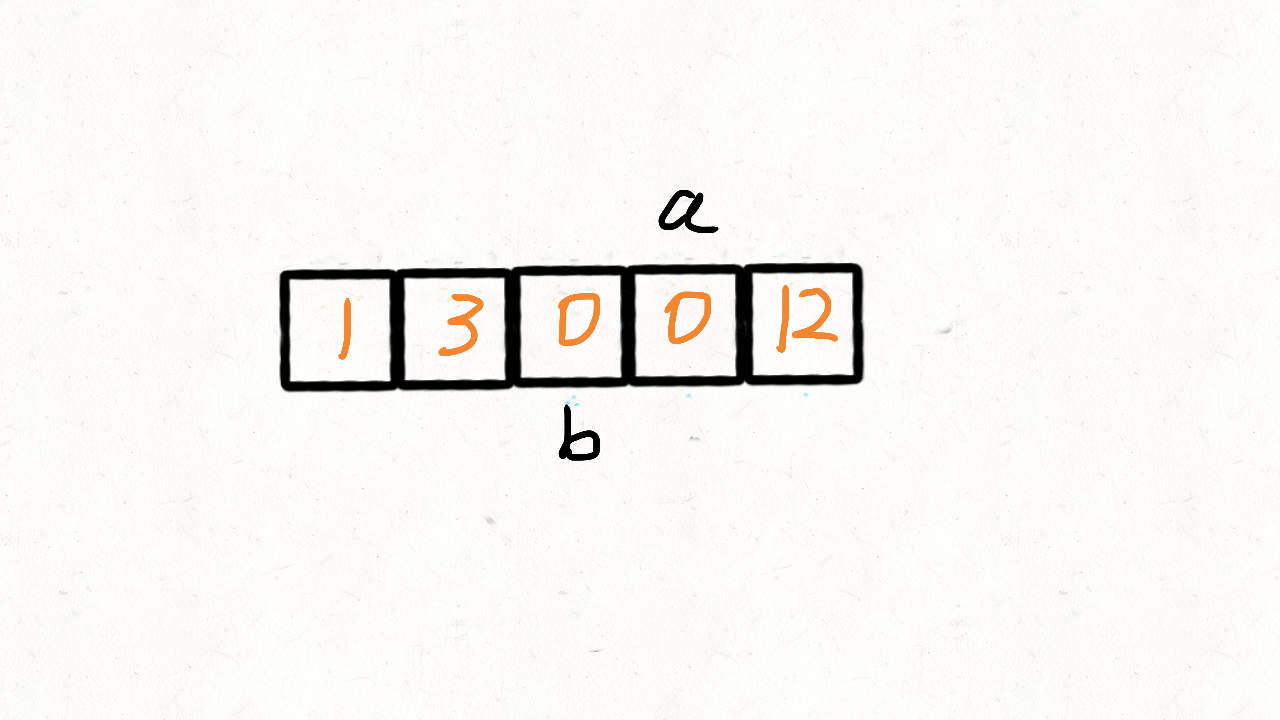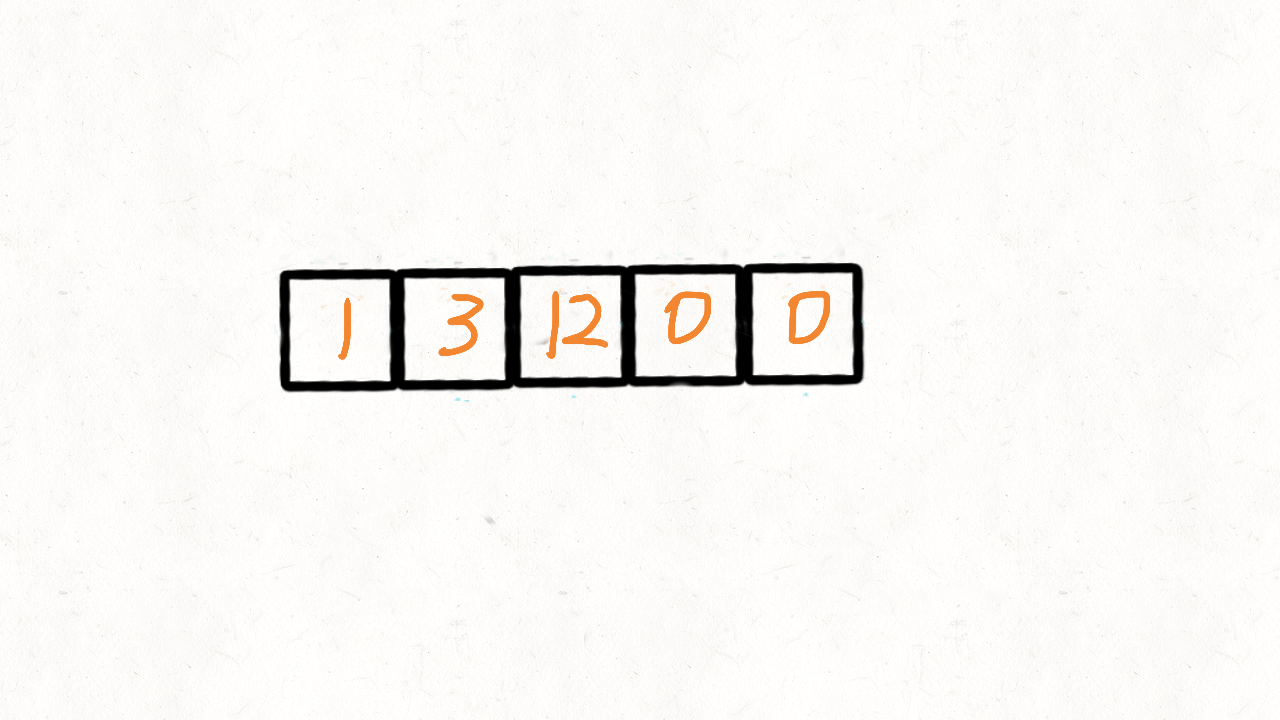数组

发表于 更新于 分类于 阅读次数：

最大子数组和[🔥350]

题目：就是给你一个大数组，然返回和最大的小数组

思路：

  1. 前缀和
  2. 然后线性更新res= curPreSum - minPreSum，然后更新minPreSum

注意：

  1. res的初始化
  2. 以及前缀和数组的初始值是0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int maxSubArray(int[] nums) {
        if(nums.length == 1) return nums[0];
       int []preSum = getPreSum(nums); 
       //找最大的和，那么就找最小前缀和 不断更新
       //System.out.println(Arrays.toString(preSum));
       int minPreSum=0;
       int res=Integer.MIN_VALUE;;
       for(int i=1;i<=nums.length;i++){
          res = Math.max(res,preSum[i]-minPreSum);
          minPreSum = Math.min(preSum[i],minPreSum);
       }
       return res;
    }
    public int[] getPreSum(int []nums){
        int []res =new int[nums.length+1];
        res[0]=0;
        for(int i=1;i<=nums.length;i++){
            res[i]=nums[i-1]+res[i-1];
        }
        return res;
    }
}

搜索旋转排序数组[🔥285]

题目：从一个部分有序的数组中以logN的时间复杂度找数

思路：

  1. 有序中找东西就应该想到用二分查找，部分有序也是如此
  2. 部分有序就对此进行拆分嘛，分类讨论，左有序，还是右序
  3. 然后在各自的有序区域内进行搜索

https://chatgpt.com/s/t_68c997c4d3948191a4497c009540388e

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
    public int search(int[] nums, int target) {
        int l = 0;
        int r = nums.length - 1;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if (nums[mid] == target) {
                return mid;
            }
            //如果 nums[mid] >= nums[l]，说明左半边有序,否则右半边有序
            //例如 [4,5,6,7,0,1,2]，如果 mid 在前半段，那 [l...mid] 一定是升序。
            //第一个if就起到寻找 有序区间的作用
            if (nums[mid] >= nums[l]) {
                //判断是否在这个左的单调区间内
                // l.......mid
                if (target >= nums[l] && target <= nums[mid]) {
                    r = mid - 1;
                } else
                    l = mid + 1;
            }
            
            else {
                //判断是否在这个右的单调区间内
                //// mid.......r
                if (target <= nums[r] && target >= nums[mid]) {
                    l = mid + 1;
                } else
                    r = mid - 1;
            }
        }
        return -1;
    }
}

扩展：

这道题要注意：如果面试官问你再旋转一次怎么做，做法还是一样的，无论旋转几次，最多只有2段递增序列

难度加强版：https://leetcode.cn/problems/search-rotate-array-lcci/description/

字节一面对这一题做了改造，如果target存在返回target，如果target不存在，返回 > target的最小值

维护一个>target的最小值

if (nums[mid] > target) {

// nums[mid] 是一个候选答案

if (ans == null || nums[mid] < ans) {

ans = nums[mid];

}

}

合并两个有序数组[🔥267]

题目：两个有序数组，然后合并成一个

思路：

  1. 三指针+从后向前遍历，p1，p2，p3

  2. 优先级队列

  3. 排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int p1=m-1;
        int p2=n-1;
        int p3=m+n-1;
        //  1 2 3 6 , 3 4 5
        while(p1>=0&&p2>=0){
            if(nums1[p1]>=nums2[p2]){
              nums1[p3]=nums1[p1];
              p1--;
            }
            else {
                nums1[p3]=nums2[p2];
                p2--;
            }
            p3--;
        }
        while(p2>=0){
            nums1[p3]=nums2[p2];
            p3--;
            p2--;
        }
        while(p1>=0){
            nums1[p3]=nums1[p1];
            p3--;
            p1--;
        }

    }
}

买卖股票的最佳时机[🔥257]

题目：实现最低买入，最高卖出

思路：贪心，肯定是得选最低价的天买入，维护一个最小值即可。

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int maxProfit(int[] prices) {
        int res=0;
        //肯定是得选最低价的天买入
        int minPrice =Integer.MAX_VALUE;
        for(int i=0;i<prices.length;i++){
            res=Math.max(res,prices[i]-minPrice);
            minPrice=Math.min(minPrice,prices[i]);
        }
        return res;
    }
}

https://leetcode-cn.com/circle/article/qiAgHn/，这篇文章讲的很通俗易懂，把几种情形都包括了

螺旋矩阵[238]

题目：顺时针螺旋顺序遍历二维数组

思路：

  1. 维护四个变量，然后模拟四个方向，通过 i 指针for循环遍历
  2. 注意边界问题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
import java.util.*;

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        int m = matrix.length;        // 行数
        int n = matrix[0].length;     // 列数

        // 定义四个边界
        int up = 0, down = m - 1;
        int left = 0, right = n - 1;

        List<Integer> res = new ArrayList<>();

        // 循环条件：还没有遍历完整个矩阵
        while (left <= right && up <= down) {

            // 1. 从左到右，遍历上边界
            for (int i = left; i <= right && res.size() < m * n; i++) {
                res.add(matrix[up][i]);
            }

            // 2. 从上到下，遍历右边界（注意不包含 corner）
            for (int i = up + 1; i <= down - 1 && res.size() < m * n; i++) {
                res.add(matrix[i][right]);
            }

            // 3. 从右到左，遍历下边界
            for (int i = right; i >= left && res.size() < m * n; i--) {
                res.add(matrix[down][i]);
            }

            // 4. 从下到上，遍历左边界（注意不包含 corner）
            for (int i = down - 1; i >= up + 1 && res.size() < m * n; i--) {
                res.add(matrix[i][left]);
            }

            // 缩小边界，进入下一圈
            left++;
            right--;
            up++;
            down--;
        }

        return res;
    }
}

合并区间[206]

题目：把多个区间，如果重叠的，就合并成多个

思路：

  1. 左端点进行排序
  2. 初始化List<int[]> tempList
  3. 然后再比较Cur区间左断点是否小于前一个区间的右断点，是的话就更新tempList里的前一个区间的右断点，不是就加入tempList
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public int[][] merge(int[][] intervals) {
        //排序
        //把情况进行一个合并
        //[2,5]
        //   [4,6]

        Arrays.sort(intervals,(iv1,iv2)->(iv1[0]-iv2[0]));
        List<int []> temp=new ArrayList<>();
        for(int []interval:intervals){
            int size=temp.size();
            //存在交集
            //执行合并逻辑
            //[  ]
            //  [    ]
            if(size>0&&interval[0]<=temp.get(size-1)[1]){
                temp.get(size-1)[1]=Math.max(interval[1],temp.get(size-1)[1]);
            }
            //无法合并就加入
            else temp.add(interval);


        }
        return temp.toArray(new int[temp.size()][2]);
    }
}

接雨水[183]

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

题目：找凹进去最多的区域

思路：

  1. 什么决定了雨水最多能装多少，即最高左边界，最高右边界
  2. OK，明白以上两点，我们就可以通过双指针来遍历，找出最高左边界，以及右边界
  3. 但实际雨水能装多少，还得决定于这段区间内的空格有多少，如何更新求出空格个数呢？

最高边界-当前位置高度即 可以装水的空格

最高边界是哪个边界？短板效应，即能装多少水取决于最短的最高边界

  1. 维护一个res，res+=当前位置装水空格
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int trap(int[] height) {
        int leftMax=0;
        int rightMax=0;
        int r=height.length-1;
        int l=0;
        int res=0;
        while(l<r){
            leftMax=Math.max(leftMax,height[l]);
            rightMax=Math.max(rightMax,height[r]);
            //哪边小先计算哪边，因为木桶效应，装水取决于短的那边
            int water= leftMax<rightMax? leftMax-height[l++]:rightMax-height[r--];
            res+=water;
        }
        return res;
    }
}

寻找两个正序数组的中位数[156]

看不懂，先摆着

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public double findMedianSortedArrays(int[] A, int[] B) {
        int m = A.length, n = B.length;
        // 保证在短数组上二分
        if (m > n) return findMedianSortedArrays(B, A);

        int left = 0, right = m;
        int halfLen = (m + n + 1) / 2;

        while (left <= right) {
            int i = (left + right) / 2;       // A 的划分位置
            int j = halfLen - i;              // B 的划分位置

            int A_left = (i == 0) ? Integer.MIN_VALUE : A[i-1];
            int A_right = (i == m) ? Integer.MAX_VALUE : A[i];
            int B_left = (j == 0) ? Integer.MIN_VALUE : B[j-1];
            int B_right = (j == n) ? Integer.MAX_VALUE : B[j];

            if (A_left <= B_right && B_left <= A_right) {
                // 找到正确划分
                int maxLeft = Math.max(A_left, B_left);
                if ((m + n) % 2 == 1) return maxLeft;
                int minRight = Math.min(A_right, B_right);
                return (maxLeft + minRight) / 2.0;
            } 
            else if (A_left > B_right) right = i - 1; // i 太大
            else left = i + 1;                        // i 太小
        }
        return 0.0;
    }
}

下一个排列[132]

题目：给你一个数组，该数组构成一个数字，找到比该数字大的最小值，且该最小值里数必须是数组里面的

arr =

  • 例如，arr = [1,2,3] 的下一个排列是 [1,3,2] 。

必须原地修改，只允许使用额外常数空间。

开背吧

思路：

  1. 纯纯找规律
  2. 从右到左 找到递增的边界。eg：[1,2,4,3,1] 那边边界就是2，我们mark为x
  3. 然后还是从右到左找到 x 右边最小大于x的数 y。eg：[1,2,4,3,1] y为3
  4. 然后交换x和y的位置。eg：[1,2,4,3,1] —> [1,3,4,2,1]
  5. reverse(原x位置，n-1)，如果第二步找不到x即x=-1，然后就直接跳这一步。eg：[1,2,4,3,1] —> [1,3,1,2,4]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
    public void nextPermutation(int[] nums) {
        int n = nums.length;

        // 第一步：从右向左找到第一个小于右侧相邻数字的数 nums[i]
        int i = n - 2;
        while (i >= 0 && nums[i] >= nums[i + 1]) {
            i--;
        }

        // 如果找到了，进入第二步；否则跳过第二步，反转整个数组
        if (i >= 0) {
            // 第二步：从右向左找到 nums[i] 右边最小的大于 nums[i] 的数 nums[j]
            int j = n - 1;
            while (nums[j] <= nums[i]) {
                j--;
            }
            // 交换 nums[i] 和 nums[j]
            swap(nums, i, j);
        }

        // 第三步：反转 [i+1, n-1]（如果上面跳过第二步，此时 i = -1）
        reverse(nums, i + 1, n - 1);
    }

    private void swap(int[] nums, int i, int j) {
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }

    private void reverse(int[] nums, int left, int right) {
        while (left < right) {
            swap(nums, left++, right--);
        }
    }
}

作者：灵茶山艾府
链接：https://leetcode.cn/problems/next-permutation/solutions/3621022/jiao-ni-cong-ling-kai-shi-si-kao-zhe-ti-9qfrq/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

上一个排列解法只需要改变两点：1.大于号换成小于号2.排降序

缺失的第一个正数[108]

题目：目标数据[1,2,3,4,5,6……] ，让你找出缺失的第一个正数

思路：

  1. 先把有的整理一遍，寻找i这个位置上对的人 nums[i] != nums[nums[i] - 1]
  2. 然后for循环找出来
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int firstMissingPositive(int[] nums) {
        //先把元素交换到正确的位置上
        for (int i = 0; i < nums.length; i++) {
            //while循环在干什么？ 在寻找i这个位置上对的人！！！！ 
            //即 i 上应该坐着 i+1 即 nums[i] == nums[nums[i]-1】 => i = nums[i] - 1
            while (nums[i] > 0 
                   && nums[i] <= nums.length 
                   && nums[i] != nums[nums[i] - 1]) {
                
                int temp = nums[nums[i] - 1];
                nums[nums[i] - 1] = nums[i];
                nums[i] = temp;
                
            }
        }
        //System.out.println(Arrays.toString(nums));
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] != i + 1) {
                return i + 1;
            }
        }
        return nums.length + 1;
    }
}

从前序与中序遍历序列构造二叉树[🔥105]

思路：

//1.从前序遍历里确定根节点
//2.然后确立根节点在中序遍历的位置 index，然后从中序遍历数组中得出 左子树的长度
//3.切分中序数组，切出来左子树，右子树 eg：[9,3,15,20,7] -> [9] [15,20,7] [0,leftSize) leftSize [leftSize-1,n)
// 4.切分前序数组，切出来左子树，右子树 eg：[3,9,20,15,7] -> [1,1+leftSize) [1+leftSize,n)
//5.递归,求出left,right
//6. return TreeNode (preOrder[0],left,right)

PS：md是真的晕递归啊啊，为什么学了两年还是晕。。。。你理解递归不要陷入细节，先明白方法返回的是什么！！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        //[3,9,20,15,7]
        //[9,3,15,20,7]

        //1.从前序遍历里确定根节点
        //2.然后确立根节点在中序遍历的位置 index
        //3.切分中序数组，切出来左子树，右子树 eg：[9,3,15,20,7] -> [9] [15,20,7] [0,leftSize) leftSize [leftSize-1,n)
        // 4.切分前序数组，切出来左子树，右子树 eg：[3,9,20,15,7] -> [1,1+leftSize) [1+leftSize,n)
        //5.递归,求出left,right
        //6. return TreeNode (preOrder[0],left,right)
        int n = preorder.length;
        if (n == 0) {
            return null;
        }
        //
        int leftSize = getLeftSize(inorder, preorder[0]);
        int[] pre1 = Arrays.copyOfRange(preorder, 1, 1 + leftSize);
        int[] pre2 = Arrays.copyOfRange(preorder, 1 + leftSize, n);
        //[0 leftSize-1] [leftSize+1 n]
        int[] in1 = Arrays.copyOfRange(inorder, 0, leftSize);
        int[] in2 = Arrays.copyOfRange(inorder, 1 + leftSize, n);
        TreeNode left = buildTree(pre1, in1);
        TreeNode right = buildTree(pre2, in2);
        return new TreeNode(preorder[0], left, right);
    }

    public int getLeftSize(int[] order, int x) {
        for (int i = 0;; i++) {
            if (order[i] == x) {
                return i;
            }
        }
    }
}

子集[99]

思路：

  1. 回溯三部曲

做的时候脑子要有回溯树

1
2
3
4
5
6
7
8
9
10
               []                      (startIndex=0)
       /         |          \
     [1]        [2]        [3]         (分别选择 1,2,3)

    /   \        / \         \
[1,2] [1,3]  [2,3]  ···     ···        (继续往右走)

   /
[1,2,3]                         (完整路径)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    List<Integer> path = new ArrayList<>();
    List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> subsets(int[] nums) {
        if (nums.length == 0) {
            return res;
        }
        dfs(nums, 0);
        return res;

    }
    //startIndex 的作用是控制
    //     startIndex 的本质是：
    
    // 限制递归的选择范围（只能往后，不回头）。
    
    // 保证子集不重复（避免 [2,1] 这种情况）。
    public void dfs(int[] nums, int startIndex) {
        res.add(new ArrayList<>(path));
        for (int i = startIndex; i < nums.length; i++) {
            path.add(nums[i]);
            dfs(nums, i + 1);
            path.remove(path.size() - 1);
        }
    }
}

时间复杂度 O（N*N）

在排序数组中查找元素的第一个和最后一个位置[93]

思路：

  1. 二分找左右边界
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class Solution {
    public int[] searchRange(int[] nums, int target) {
        //二分查找
        int leftBorder=leftBorder(nums,target);
        int rightBorder=rightBorder(nums,target);
        if(leftBorder==-1&&rightBorder==-1){
           return new int[]{leftBorder,rightBorder};
        }
        else 
        return new int[]{leftBorder+1,rightBorder-1};
        
    }
    public int leftBorder(int []nums,int target){
        int left=0;
        int right=nums.length-1;//左闭右闭
        int leftBorder=-1;
        while(left<=right){
            int mid=left+(right-left)/2;
            if(nums[mid]==target){
               right=mid-1;
               leftBorder=right;
            }
            else if(nums[mid]<target){
                left=mid+1;
            }
            else if(nums[mid]>target){
                right=mid-1;
            }
        }
        return leftBorder;
    }
    public int rightBorder(int []nums,int target){
        int left=0;
        int right=nums.length-1;//左闭右闭
        int rightBorder=-1;
        while(left<=right){
            int mid=left+(right-left)/2;
            if(nums[mid]==target){
               left=mid+1;
               rightBorder=left;
            }
            else if(nums[mid]<target){
                left=mid+1;
            }
            else if(nums[mid]>target){
                right=mid-1;
            }
        }
        return rightBorder;
    }
}

组合总和[86]

题目：给一个数组，然后给一个target，让你求和等于target的 数组里的数字组合，每个数字可重复取

思路：

  1. 回溯
  2. 重复取怎么处理呢 dfs(candidates,target,i);不是i+1， i就表示可以重复取。然后用sum>target来控制 超过就return
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    List<Integer> path = new ArrayList<>();
    List<List<Integer>> res = new ArrayList<>();
    int sum =0;//用来记录cur和
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        dfs(candidates,target,0);
        return res;
    }
    public void dfs(int []candidates,int target,int startIndex){
        if(sum == target){
            res.add(new ArrayList<>(path));
            return ;
        }
        for(int i=startIndex;i<candidates.length;i++){
            if(sum > target) break;
            sum += candidates[i];
            path.add(candidates[i]);
            //这里的i表示 每个数可以重复选取
            dfs(candidates,target,i);
            sum -= path.remove(path.size()-1);
        }
    }
}

要考虑去重吗？

最小路径和[86]

题目

思路：

  1. 多条路径求最小和的，可以考虑dfs算法，但很遗憾，时间复杂度2的m+n 次方，超时了
  2. 动态规划。理清数组元素含义，以及当前状态是怎么由前面的状态推导过来的

dfs：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    int res = Integer.MAX_VALUE;
    int sum = 0;
    int n, m;
    int[][] dir = {{0,1},{1,0}}; // 只需要右和下

    public int minPathSum(int[][] grid) {
        n = grid.length;
        m = grid[0].length;
        dfs(grid, 0, 0, 0);
        return res;
    }

    public void dfs(int[][] grid, int x, int y, int currentSum) {
        if(x >= n || y >= m) return; // 越界
        currentSum += grid[x][y];
        if(x == n-1 && y == m-1) {
            res = Math.min(res, currentSum);
            return;
        }
        dfs(grid, x+1, y, currentSum); // 下
        dfs(grid, x, y+1, currentSum); // 右
    }
}

动态规划

美团一面，写完要求在源码基础上生成路径？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
public int minPathSum(int[][] grid) {
        int n = grid.length;
        int m = grid[0].length;

        int[][] dp = new int[n][m];         // dp[i][j] = 到 (i,j) 的最小路径和
        String[][] path = new String[n][m]; // path[i][j] = 到 (i,j) 的路径字符串

        dp[0][0] = grid[0][0];
        path[0][0] = "(0,0)";

        // 初始化第一列
        for (int i = 1; i < n; i++) {
            dp[i][0] = dp[i-1][0] + grid[i][0];
            path[i][0] = path[i-1][0] + " -> (" + i + "," + 0 + ")";
        }

        // 初始化第一行
        for (int j = 1; j < m; j++) {
            dp[0][j] = dp[0][j-1] + grid[0][j];
            path[0][j] = path[0][j-1] + " -> (" + 0 + "," + j + ")";
        }

        // 填表
        for (int i = 1; i < n; i++) {
            for (int j = 1; j < m; j++) {
                //下走 还是 左走
                if (dp[i-1][j] < dp[i][j-1]) {
                    dp[i][j] = dp[i-1][j] + grid[i][j];
                    path[i][j] = path[i-1][j] + " -> (" + i + "," + j + ")";
                } else {
                    dp[i][j] = dp[i][j-1] + grid[i][j];
                    path[i][j] = path[i][j-1] + " -> (" + i + "," + j + ")";
                }
            }
        }

        System.out.println("Path: " + path[n-1][m-1]);
        return dp[n-1][m-1];
    }

最长连续序列[82]

题目：从一没排好序的数组里找出 最长的连续序列 如 1,2,3,4

思路：

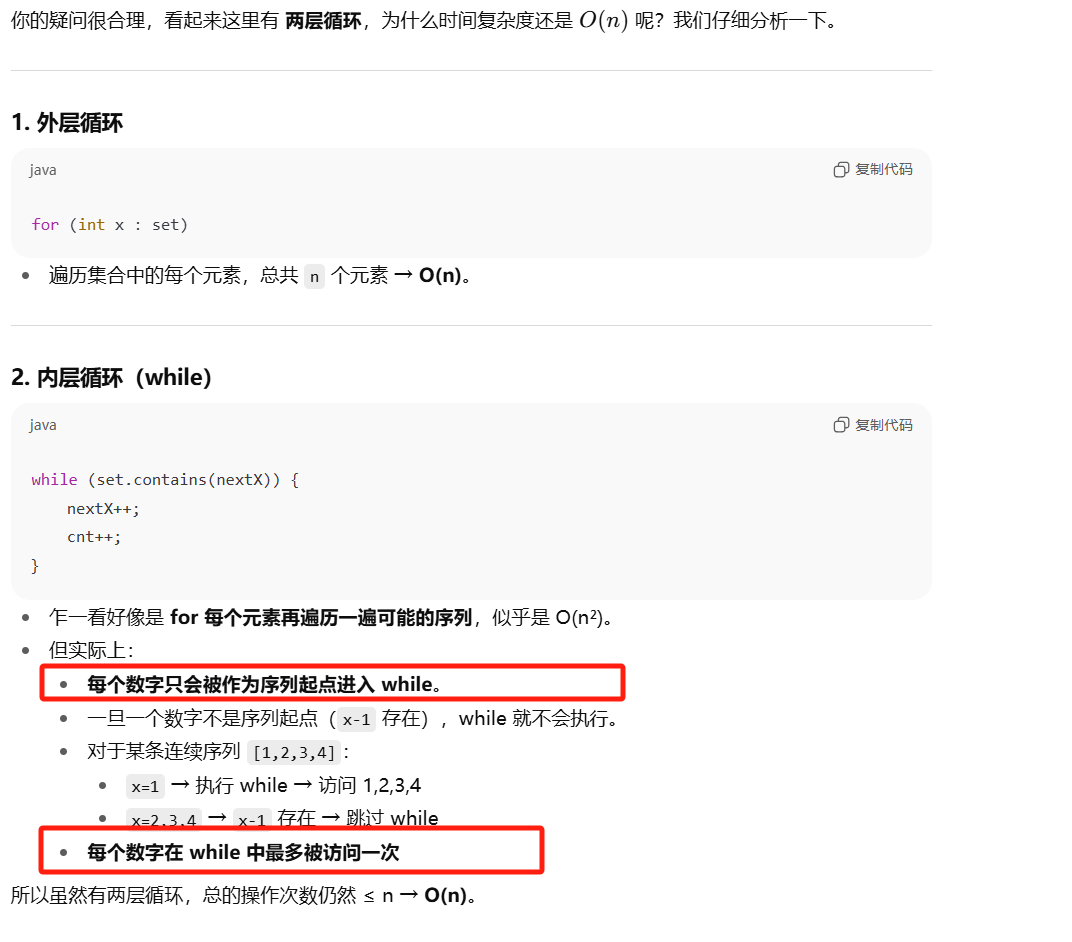
  1. hashset，for x 然后以x为开头搜连续段，后续for 时候如果遇到连续段里的就 continue 。即哈希set，每次搜索一个数搜完一个连续段，后面在遇到连续段中的直接跳过。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public int longestConsecutive(int[] nums) {
        Set<Integer> set = new HashSet<>();
        //去重
        for (int i : nums) {
            set.add(i);
        }
        //
        int res = 0;
        for (int x : set) {
            //已经找过的 就不要再找了
            if (set.contains(x - 1))
                continue;

            //寻找以x为开头的连续序列
            //x x+1 x+1+1 ....
            int cnt = 1;
            int nextX = x + 1;
            while (set.contains(nextX)) {
                nextX++;
                cnt++;
            }
            res = Math.max(res, cnt);
        }
        return res;
    }
}

时间复杂度：O N，因为每个元素只被访问了一次

旋转图像[]

思路：

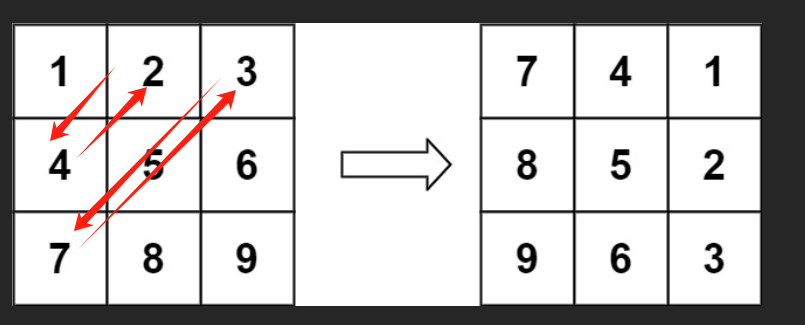
  1. 先交换行（上下倒转），然后转置（ 转置操作：matrix[i][j] ↔ matrix[j][i]）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length - 1;
        int m = matrix[0].length - 1;
        //先交换行 上下倒置 第一行 和 第n 行 第二行 和 第 n-1行
        for (int i = 0; i <= n/2; i++) {
            int[] temp = matrix[i];
            matrix[i] = matrix[n - i];
            matrix[n - i] = temp;
        }
        //倒置 [i][j] 和 [j][i] 交换 对角想交换
        for (int i = 0; i <= n; i++) {
            for (int j = i + 1; j <= m; j++) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
    }
}

转置：

岛屿的最大面积[80]

思路：

  1. 就是dfs，模版题，没啥好说的，需要注意一下这种情况因为是四面八方都可以走，那就得记录走过的位置或者说 for循环入口其实导向是同一块岛屿
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    int area = 0;
    int res = 0;

    public int maxAreaOfIsland(int[][] grid) {
        //bfs or dfs

        //dfs
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                area = 0;
                dfs(grid, i, j);
                res = Math.max(res, area);
            }
        }
        return res;
    }

    public void dfs(int[][] grid, int x, int y) {
        if (x < 0 || y < 0 || x >= grid.length || y >= grid[0].length) {
            return;
        }
        if (grid[x][y] != 1) {
            return;
        }
        if (grid[x][y] == 1)
            area++;
        grid[x][y] = -1;

        dfs(grid, x + 1, y);
        dfs(grid, x, y + 1);
        dfs(grid, x, y - 1);
        dfs(grid, x - 1, y);
    }
}

寻找峰值[76]

题目：找出山峰，返回山峰的索引

思路：二分查找，分情况讨论

1
2
3
4
5
6
7
8
9
10
11
12
// [-无穷 ...3 4 .... -无穷]
// 那么4的右侧一定有山峰
// mid = indexof(3)
if (nums[mid] < nums[mid + 1]) {
    l = mid + 1;
}
// [-无穷 ...4 3 .... -无穷]
// mid = indexof(3)
// 那么4的左侧一定有山峰
else {
    r = mid - 1;
}

图解：162. 寻找峰值 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public int findPeakElement(int[] nums) {
        if (nums.length == 1)
            return 0;
        //两端
        if (nums[nums.length - 1] > nums[nums.length - 2]) {
            return nums.length - 1;
        }
        if (nums[0] > nums[1]) {
            return 0;
        }
        //二分法
        int l = 0;
        int r = nums.length - 1;
        while (l <= r) {
            int mid = (r + l) / 2;
            // [-无穷 ...3 4 .... -无穷]
            // 那么4的右侧一定有山峰
            // mid = indexof(3)
            if (nums[mid] < nums[mid + 1]) {
                l = mid + 1;
            }
            // [-无穷 ...4 3 .... -无穷]
            // mid = indexof(3)
            // 那么4的左侧一定有山峰
            else {
                r = mid - 1;
            }
        }
        return l;
    }
}

乘积最大子数组[70]

多数元素[67]

思路：

  1. map
  2. 空间复杂度O（1）的解法：摩尔投票

长度最小的子数组

题目：长度最小的和为k的子数组

思路：

移动零[60]

思路：

  1. 双指针，i0，i
  2. 记录0元素的位置i0，i。如果nums[i]为非0元素，就与其交换，然后i0++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public void moveZeroes(int[] nums) {
        //双指针
        int i0 = 0;// i0表示指向
        for (; i0 < nums.length; i0++) {
            if (nums[i0] == 0) {
                break;
            }
        }
        //[1,2,0,5,6,0,1]
        //
        for (int i = i0 + 1; i < nums.length; i++) {
            // 非0 元素与0元素交换
            if (nums[i] != 0) {
                // i0 i交换
                int temp = nums[i];
                nums[i] = nums[i0];
                nums[i0] = temp;
                // 交换过了 i0++
                i0++;
            }
        }
    }
}

寻找旋转排序数组中的最小值[56]

题目：在部分有序数组中找到最小值

思路：

  1. 看到log N的算法，就得想到二分
  2. 根据mid和nums.length元素比较 得出最小值是在右边还是在左边
  3. [3,4,5,1,2]：最小值在右边
  4. [1 2 3 4 5]：最小值在左边
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int findMin(int[] nums) {
        //
        int l = 0;
        int r = nums.length - 1;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            // [3,4,5,1,2]  5 > 2 最小值在右边
            // 为什么不能和nums[0] 比较? 因为无法区分 [1 2 3 4 5] [3,4,5,1,2] 这两种情况
            if (nums[mid] > nums[nums.length - 1]) {
                l = mid +1;
            } else {
                //[1 2 3 4 5] 最小值在右边
                r = mid -1;
            }
        }
        
        return nums[l];
    }
}

先升序再降序的数组，找到最大值

参考寻找峰值

单词搜索[54]

思路：

  1. dfs+回溯
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
    int offset = -1;
    boolean[][] visited;

    public boolean exist(char[][] board, String word) {
        visited = new boolean[board.length][board[0].length];
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[0].length; j++) {
                if (dfs(board, i, j, word, 0)) {
                    return true;
                }
            }
        }
        return false;
    }

    public boolean dfs(char[][] board, int x, int y, String word, int offset) {
        if (x < 0 || y < 0 || x >= board.length || y >= board[0].length) {
            return false;
        }
        if (visited[x][y])
            return false;
        
        if (board[x][y] != word.charAt(offset)) {
            return false;
        }
        if (offset == word.length() - 1)
            return true;

        visited[x][y] = true;

        boolean found = dfs(board, x, y + 1, word, offset + 1) ||
                dfs(board, x + 1, y, word, offset + 1) ||
                dfs(board, x, y - 1, word, offset + 1) ||
                dfs(board, x - 1, y, word, offset + 1);
        //回溯
        visited[x][y] = false;
        return found;
    }
}

分隔链表[20]

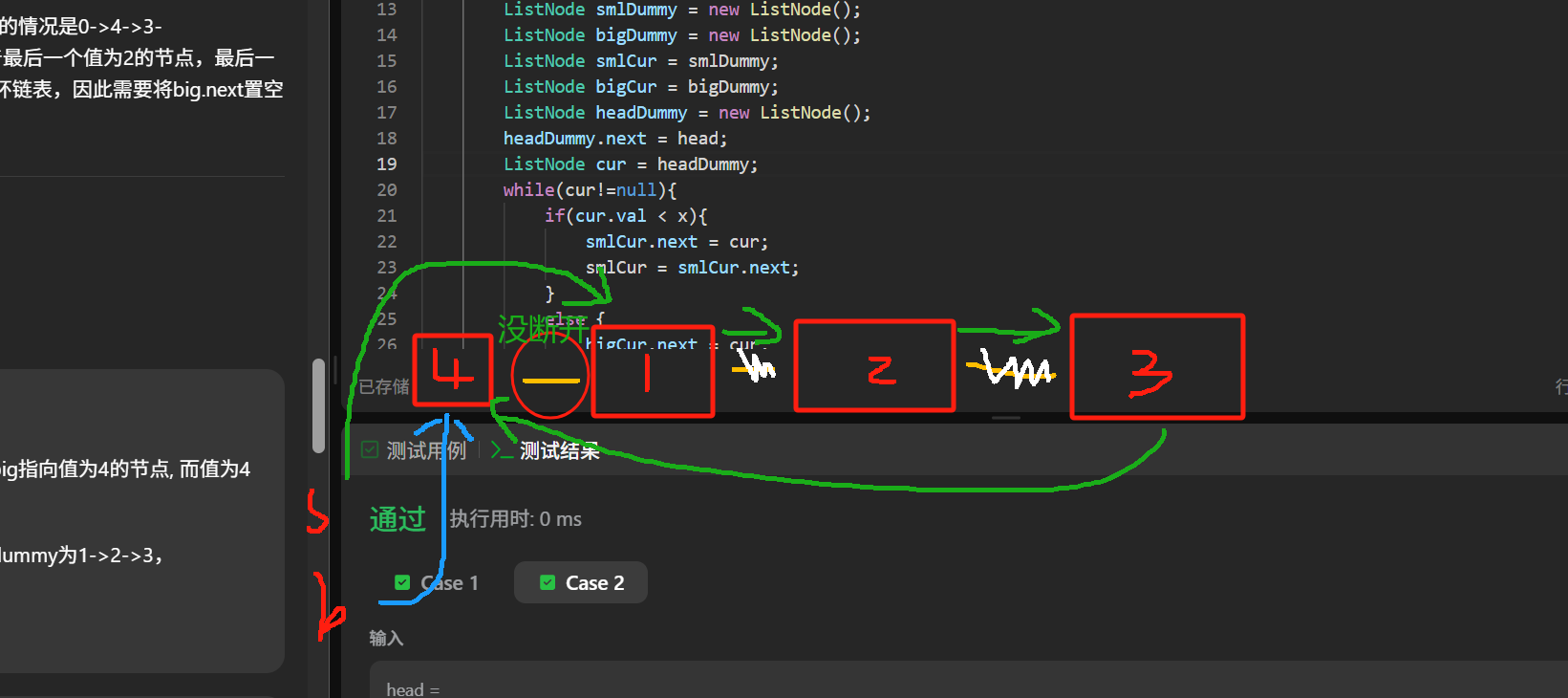
思路：

  1. 双指针，sml，big
  2. if cur < x 加入sml，else 加入big

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode partition(ListNode head, int x) {
        ListNode smlDummy = new ListNode();
        ListNode bigDummy = new ListNode();
        ListNode smlCur = smlDummy;
        ListNode bigCur = bigDummy;
        ListNode cur = head;
        while(cur!=null){
            if(cur.val < x){
                smlCur.next = cur;
                smlCur = smlCur.next;
            }
            else {
                bigCur.next = cur;
                bigCur = bigCur.next;
            }
            cur = cur.next;
        }
        smlCur.next = bigDummy.next;
        //重点
        bigCur.next = null;
        return smlDummy.next;
    }
}

搜索二维矩阵 II[80]

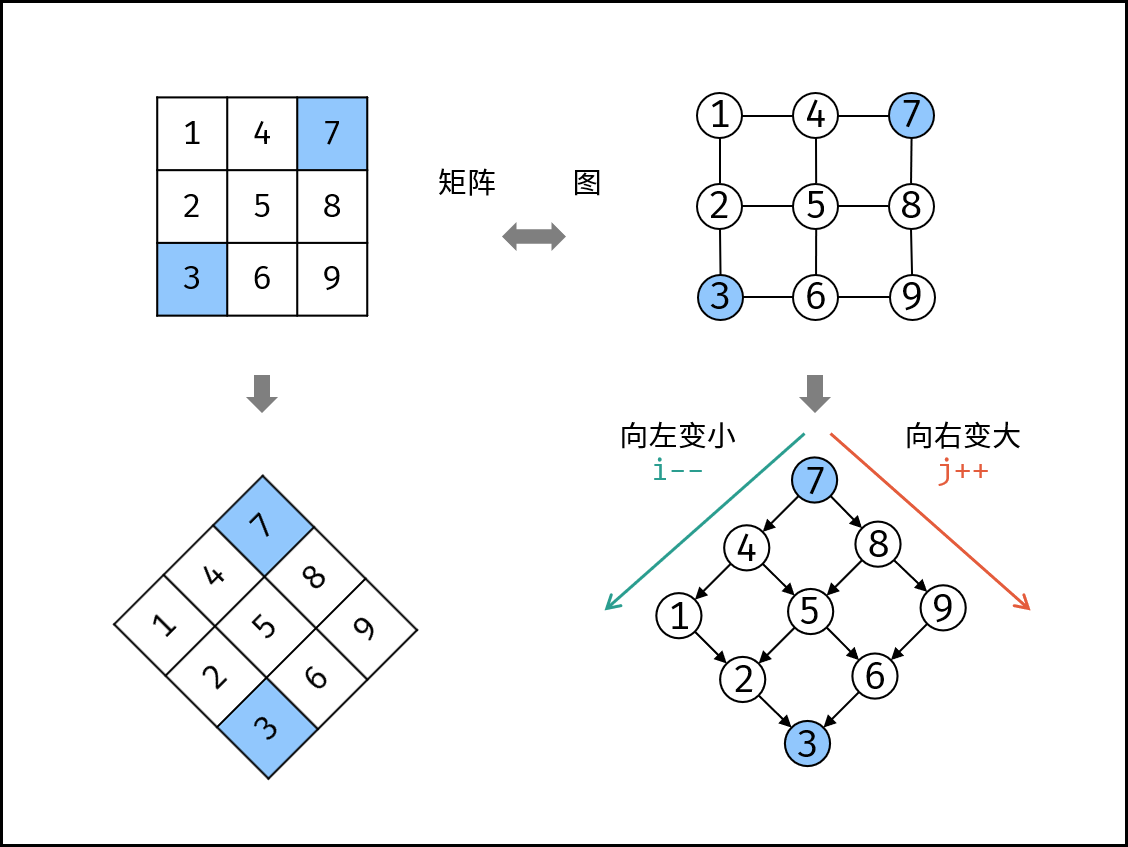
思路：旋转45度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        //逆旋转旋转45
        int i = matrix.length - 1;
        int j = 0;
        while(i >= 0 && j < matrix[0].length){
            if(matrix[i][j] > target){
                //向左变小
                i--;
            }
            else if(matrix[i][j] < target){
                //向右变大
                j++;
            }
            else return true;
        }
        return false;
        
        
    }
}

乘积最大子数组[71]

思路：

  1. 暴力，两层for循环
  2. 是不可以搞前缀积的！！！
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int maxProduct(int[] nums) {
        int res = Integer.MIN_VALUE;
        for(int i = 0; i < nums.length; i++){
            int sub = 1;
            for(int j = i; j < nums.length; j++){
                sub = sub * nums[j];
                res = Math.max(res, sub);
            }
        }
        return res;
    }
}
  1. 动态规划

维护当前最大值和当前最小值

解释：当前最大值和当前最小值是指什么？

变量 更严谨的定义
curMax 以 nums[i] 结尾的所有子数组里「乘积最大的值」，如果当前是 0，则为 0
curMin 以 nums[i] 结尾的所有子数组里「乘积最小的值」，如果当前是 0，则为 0
  1. 因为当遇到负数时，要乘上负数时，当前最大值会变成当前最小值，当前最小值会变成当前最大值
  2. 如果一直遇到整数，那么不断curMax * curNum[] 就好了
  3. 如果遇到了 0，这时候就会自动断开了，curMax = 0, curMin = 0（即重开了）

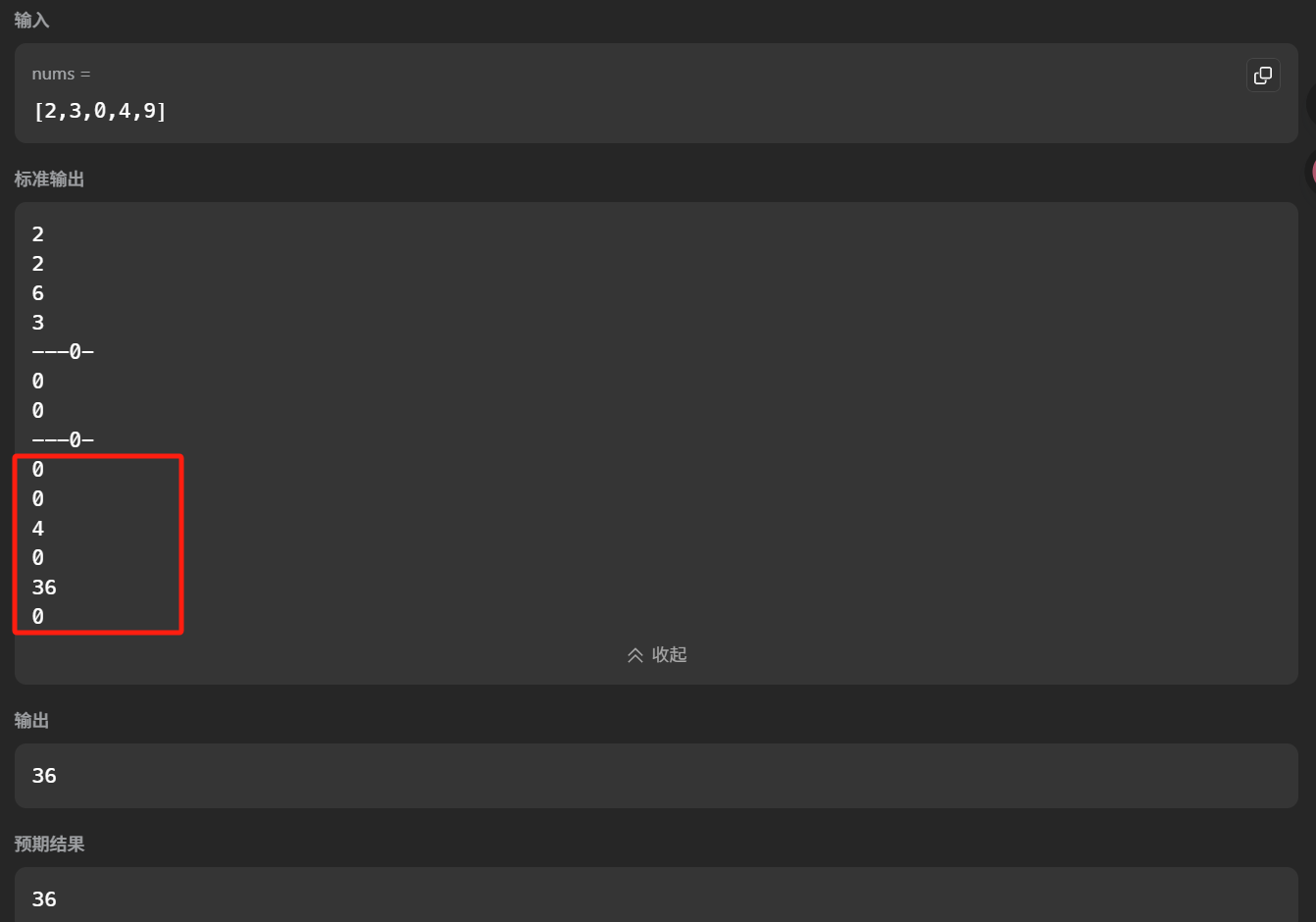
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public int maxProduct(int[] nums) {
        int res = Integer.MIN_VALUE;
        //当前最大值，最小值
        int curMax = 1;
        int curMin = 1;
        for (int i = 0; i < nums.length; i++) {
            //如果为负数，就会触发 最大值变成最小值 最小值变成最大值
            //  1 2 -5 curMax = 2 curMin = 1
            //  curMax = 1 curMin = 2
            // curMax = -5 curMin = -10 
            if (nums[i] < 0) {
                int temp = curMax;
                curMax = curMin;
                curMin = temp;
            }
            curMax = Math.max(curMax * nums[i], nums[i]);
            curMin = Math.min(curMin * nums[i], nums[i]);
            if(nums[i] == 0){
                System.out.println("---0-");
                System.out.println(curMax);
                System.out.println(curMin);
                System.out.println("---0-");
            } 
            System.out.println(curMax);
            System.out.println(curMin);
            res = Math.max(curMax, res);
        }
        return res;
    }
}

字节腾讯，还要输出这个数组

维护bestStart bestEnd，然后如果nums[i] > curMax 就会开始重新计数了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
    public int maxProduct(int[] nums) {
        int res = Integer.MIN_VALUE;
        //当前最大值，最小值
        int curMax = 1;
        int curMin = 1;
        //结果集的起始
        int start = 0, bestStart = 0, bestEnd = 0;

        for (int i = 0; i < nums.length; i++) {
            //如果为负数，就会触发 最大值变成最小值 最小值变成最大值
            //  1 2 -5 curMax = 2 curMin = 1
            //  curMax = 1 curMin = 2
            // curMax = -5 curMin = -10 
            if (nums[i] < 0) {
                int temp = curMax;
                curMax = curMin;
                curMin = temp;
            }
            if (curMax * nums[i] < nums[i]) {
                curMax = nums[i];
                start = i;
            } 
            else curMax = curMax * nums[i];
            
            curMin = Math.min(curMin * nums[i], nums[i]);
            
            if (res < curMax) {
                res = curMax;
                bestStart = start;
                bestEnd = i;
            }
        }
        System.out.println(Arrays.toString(Arrays.copyOfRange(nums, bestStart, bestEnd + 1)));
        return res;
    }
}

跳跃游戏[57]

思路：两种做法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public boolean canJump(int[] nums) {
        //i 是 人的位置，k 是路（即人能最远到达的地方），路就决定了 人能到达的位置 
        if(nums.length <= 1) return true;
        int k = 0;
        for(int i = 0; i <= k; i++){
            k = Math.max(k, nums[i] + i);
            if(k >= nums.length - 1){
                return true;
            }
        }
        return false;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public boolean canJump(int[] nums) {
        //
        if(nums.length <= 1){
            return true;
        }
        // 2 3 1 1 4
        // k表示 当前能跳到的最远位置
        int k = 0;
        for(int i = 0; i < nums.length; i++){
            if(i > k) return false;
            k = Math.max(k, i + nums[i]);
            System.out.println("当前下标：" + i + "最远位置：" + k);
        }
        return true;
    }
}

跳跃游戏 II[47]

两种做法：

  1. 动态规划
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public int jump(int[] nums) {
        if(nums.length <= 1) return nums.length - 1;
        //表示 走到i的所需的最小跳跃数
        int n = nums.length;
        int []dp = new int[n];
        Arrays.fill(dp, Integer.MAX_VALUE);
        dp[0] = 0;
        dp[1] = 1;
        for(int i = 0; i < nums.length; i++){
            //状态方程
            int k = i + nums[i];
            if( k > nums.length - 1){
                k = nums.length - 1;
            }
            
            dp[k] = Math.min(dp[k], dp[i] + 1);
            for(int j = i + 1; j < k + 1; j++){
                dp[j] = Math.min(dp[k], dp[j]);
            }
            //Arrays.fill(dp,, dp[k]);
            System.out.println(Arrays.toString(dp));

        }
        //System.out.println(Arrays.toString(dp));
        return dp[n - 1];
    }
}

时间复杂度 = O(n²)，空间复杂度 = O(n)

  1. 贪心
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int jump(int[] nums) {
        int steps = 0;      // 总跳跃次数
        int end = 0;        // 当前这一步能跳到的最远边界
        int farthest = 0;   // 下一步能跳到的最远位置

        // 注意：最后一个位置不需要再跳，所以循环到 n-2
        for (int i = 0; i < nums.length - 1; i++) {
            // 更新下一步的最远可达位置
            farthest = Math.max(farthest, i + nums[i]);

            // 如果到达当前步的边界，就必须跳一次
            if (i == end) {
                steps++;
                end = farthest;  // 更新下一跳的边界
            }
        }
        return steps;
    }
}

盛最多水的容器[51]

思路：

  1. 双指针
  2. 贪心思路: 木桶容量由短板决定, 移动长板的话, 水面高度不可能再上升, 而宽度变小了, 所以只有通过移动短板, 才有可能使水位上升.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
  public int maxArea(int[] height) {
  //双指针
  int l = 0;
  int r = height.length - 1;
  int res = Integer.MIN_VALUE;
  while(l <= r){
    int h = Math.min(height[l], height[r]);
    res = Math.max(res, h * (r - l));
    //把矮的给淘汰掉，因为要装，那么短的那表一定得尽可能长
    if(height[l] > height[r]){
      r--;
    }
    else l++;
  }
  return res;
}
}

最短无序连续子数组[10]

思路：

  1. 最简单的做法，即先排序，然后比对，从左，从右，找第一个不同的元素，然后len = right - left + 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int findUnsortedSubarray(int[] nums) {
        int[] newNums = Arrays.copyOfRange(nums, 0, nums.length);
        Arrays.sort(newNums);
        int l = 0;
        int r = -1;
        for(int i = 0;i < newNums.length; i++){
            if(newNums[i] != nums[i]){
                l = i;
                break;
            }
        }
        for(int i = newNums.length - 1;i >= 0; i--){
            if(newNums[i] != nums[i]){
                r = i;
                break;
            }
        }
        return r - l + 1 > 0? r - l + 1: 0;
    }
}

计数排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
    public int findUnsortedSubarray(int[] nums) {
        int[] newNums = Arrays.copyOfRange(nums, 0, nums.length);
        sort(newNums);
        //System.out.println(Arrays.toString(newNums));
        int l = 0;
        int r = -1;
        for(int i = 0;i < newNums.length; i++){
            if(newNums[i] != nums[i]){
                l = i;
                break;
            }
        }
        for(int i = newNums.length - 1;i >= 0; i--){
            if(newNums[i] != nums[i]){
                r = i;
                break;
            }
        }
        return r - l + 1 > 0? r - l + 1: 0;
    }
    public void sort(int []nums){
        int MAX = 100000;
        int[] counter = new int[MAX * 2 + 4];
        int min = Integer.MAX_VALUE;
        int max = Integer.MIN_VALUE;
        for(int i: nums){
            min = Math.min(i, min);
            max = Math.max(i, max);
            counter[i + MAX]++;
        }
        int idx = 0;
        for(int i = min; i <= max; i++){
            int count = counter[i + MAX];
            while(count > 0){
                nums[idx] = i;
                count--;
                idx++;
            }
        }
    }
}

任务调度器[5]

思路：

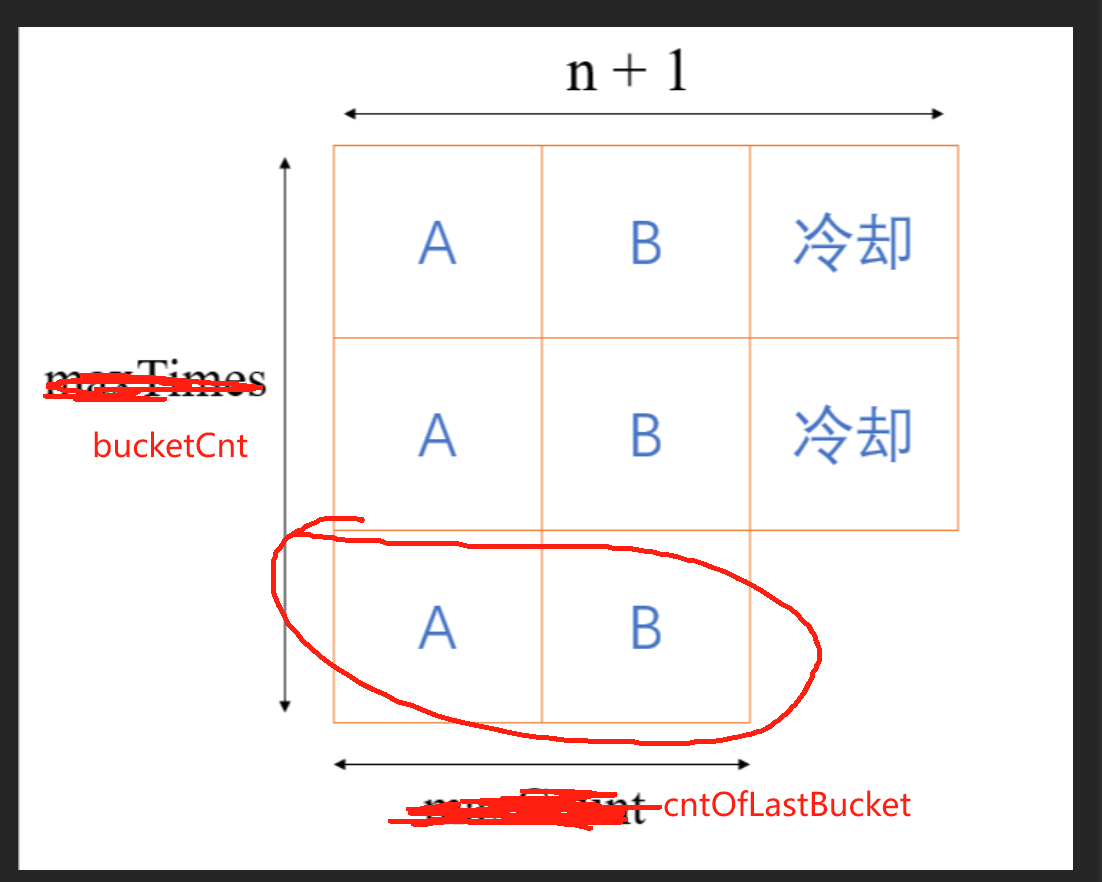
  1. 贪心：很容易想到就是 先安排出现次数最多的任务，然后让这个任务之间的间隔刚好为N

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
    public int leastInterval(char[] tasks, int n) {
        //贪心：很容易想到就是 先安排出现次数最多的任务，然后让这个任务之间的间隔刚好为N
        Map<Character,Integer> counter = new HashMap();
        for(char c: tasks){
            counter.put(c, counter.getOrDefault(c, 0) + 1);
        }
        int max = 0;
        char cMax = '*';
        for(char c: counter.keySet()){
            if(counter.get(c) > max) {
                cMax = c;
                max = counter.get(c);
            }
        }
        int bucketCnt = max;
        int cntOflastBucket = 0;
        for(char c: counter.keySet()){
            if(counter.get(c) == max) cntOflastBucket++;
        }
        //第一种情况：槽够用
        //eg：A：4 B：4 C：1 D: 1 n = 2 
        //A B C
        //A B D
        //A B *
        //A B
        //则 完成时间不能等于 长度

        //第二种情况：槽不够用
        //eg：A：4 B：4 C：4 D: 2 n = 2 
        //A B C D
        //A B C D
        //A B C 
        //A B C
        //则 完成时间等于 长度
        return Math.max((bucketCnt - 1) * (n + 1) + cntOflastBucket, tasks.length);
    }
}

找到所有数组中消失的数字[4]

同缺失的第一个正数

思路：

  1. 交换到正确的位置上
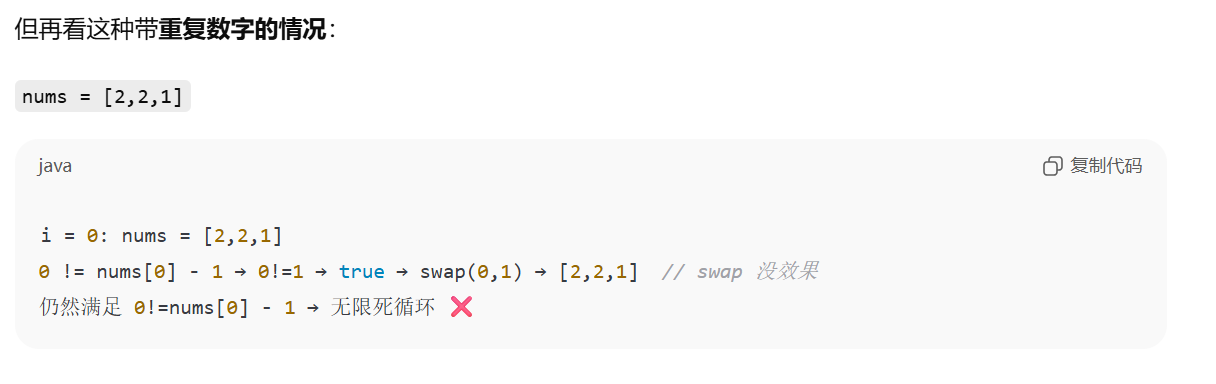
  2. [1,2,3] –> nums[i] == nums[nums[i] - 1]，即nums[0] == nums[1 - 1]。为什么不能写成 i=nums[i] - 1?

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
    public List<Integer> findDisappearedNumbers(int[] nums) {
        for(int i = 0; i < nums.length; i++){
            System.out.println(i);
            System.out.println(nums[i] +"::::::::::::" + nums[nums[i] - 1]);
            while(nums[i] <= nums.length && nums[i] != nums[nums[i] - 1]){
                System.out.println(Arrays.toString(nums));
                System.out.println(i + ":::"+ (nums[i] -1));
                swap(nums, i, nums[i] - 1);
            }
        }
        //System.out.println(Arrays.toString(nums));
        List<Integer> res = new ArrayList();
        // 1 2 3
        for(int i = 0; i < nums.length; i++){
            if(nums[i] != i + 1)
                res.add(i + 1);
        }
        return res;
    }
    public void swap(int []nums, int i,int j){
        int temp  = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}
//eg：[2,2,1] nums[i] == nums[nums[i] - 1] 表示当前数字是否在正确位置上，每次就会正确交换一次，这样子每个数字只会被遍历一次
// 0
// 2::::::::::::2
// 1
// 2::::::::::::2
// 2
// 1::::::::::::2
// [2, 2, 1]
// 2:::0

根据身高重建队列

  1. 先排序，先按p[0] 降序 and p[1] 升序。

:::info
楼主的解释很棒！但是这里稍微有点没有解释清楚，“按照第二个元素正向排序，我们希望 k 大的尽量在后面，减少插入操作的次数。”不止是为了减少插入次数，也是为了保证正确性。
举个例子，在身高一样，k不一样的时候，譬如[5,2]和[5,3], 对于最后排完的数组，[5,2]必然在[5,3]的前面。所以如果遍历的时候[5,3]在前面，等它先插入完，这个时候它前面会有3个大于等于它的数组对，遍历到[5,2]的时候，它必然又会插入[5,3]前面（因为它会插入链表索引为2的地方），这个时候[5,3]前面就会有4个大于等于它的数组对了，这样就会出错。

:::

  1. 然后巧用 add（index，n）实现插队
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int[][] reconstructQueue(int[][] people) {
        //先排序再插队
        //排序
        Arrays.sort(people,
            (a, b) -> {
                return  a[0] == b[0] ? a[1] - b[1] : b[0] - a[0];  
            }
        );
        List<int[]> res = new ArrayList();

        for(int []p: people) {
            System.out.println(Arrays.toString(p));
            //插队
            res.add(p[1], p);
        }
         System.out.println("////////////");
        for(int []p: res) {
            System.out.println(Arrays.toString(p));
        }
        return res.toArray(new int[people.length][2]);
    }
}

除自身以外数组的乘积[]

思路

  1. 前缀积，后缀积
  2. Map<Integer,Integer> front：k：当前元素index。v：包含当前元素的区间积，元素之前的积即map.getIOrDefault(i - 1, 1) * curNum
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import java.util.*;

class Solution {
    public int[] productExceptSelf(int[] nums) {
        int[] ans = new int[nums.length];
        Map<Integer, Integer> front = new HashMap<>();
        Map<Integer, Integer> back = new HashMap<>();

        // 前缀积
        for (int i = 0; i < nums.length; i++) {
            front.put(i, front.getOrDefault(i - 1, 1) * nums[i]);
        }

        // 后缀积
        for (int i = nums.length - 1; i >= 0; i--) {
            back.put(i, back.getOrDefault(i + 1, 1) * nums[i]);
        }

        // 最终结果
        for (int i = 0; i < nums.length; i++) {
            int left = front.getOrDefault(i - 1, 1);
            int right = back.getOrDefault(i + 1, 1);
            ans[i] = left * right;
        }

        return ans;
    }
}

会议室2[24]

1